In Example 3, change −119 to −88 and then find the common difference.

Data from Example 3

Find the common difference between successive terms of the arithmetic sequence for which the third term is 5 and the 34th term is −119. In order to use Eq. (19.2), we could calculate a₁, but we can also treat the third term as a₁ and the 34th term as a₃₂. This gives us the same sequence from 5 to −119. Therefore, using the values a₁ = 5, a₃₂ = −119 and n = 32, we can find the value of d. Substituting these values in Eq. (19.2) gives

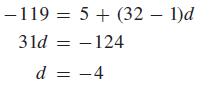
There is no information as to whether this is a finite or an infinite sequence. The solution is the same in either case

-119 5+ (32-1)d 31d = -124 d = 4