In Example 5, change the third equation of the second system to 5x + 3y = 11.

Data from Example 5

Solve the following systems of equations by Gaussian elimination. The solutions are shown at the left. We note that each system has three equations and two unknowns. In the solution of the first system, the third equation becomes 0 = 0, and only two equations are needed to find the solution x = 1, y = 2. In the solution of the second system, the third equation becomes 0 = −4, which means the system is inconsistent and there is no solution.

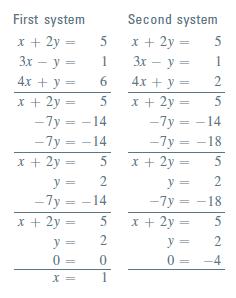
Graphing the systems, note that in Fig. 16.17, each of the lines passes through the point (1, 2), whereas in Fig. 16.18, there is no point common to the three lines.

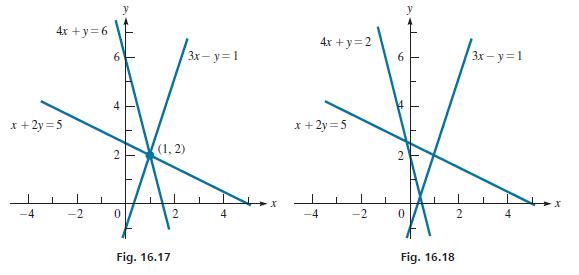
First system x + 2y = 3x - y = 4x + y = x + 2y = x + 2y = -7y=-14 -7y=-14 5 1 x + 2y = 6 5 y = 0 5 y = -7y=-14 2452 5 0 Second system x + 2y = 3x - y = 4x + y = x + 2y = -7y=-14 -7y=-18 x + 2y = 5 1 2 5 x + 2y y = -7y=-18 y = 0 5 2 5 52 2 -4