Make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 4, change x to 2x in the second equation and then solve the system of equations.

Data from Example 4

Use the method of addition or subtraction to solve the following system of equations.

3x − 2y = 4

x + 3y = 2

Looking at the coefficients of x and y, we see that we must multiply the second equation by 3 to make the coefficients of x the same. To make the coefficients of y numerically the same, we must multiply the first equation by 3 and the second equation by 2. Thus, the best method is to multiply the second equation by 3 and eliminate x. CAUTION Be careful to multiply the terms on both sides: a common error is to forget to multiply the value on the right. ■ After multiplying, the coefficients of x have the same sign. Therefore, we subtract terms of the second equation from those of the first equation:

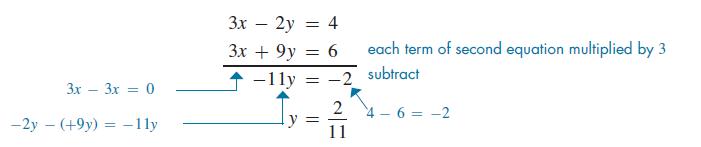
In order to find the value of x, substitute y = 2/11 into one of the original equations. Choosing the second equation (its form is somewhat simpler), we have

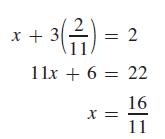
Therefore, the solution is x = 16/11, y = 2/11. Substituting these values into both of the original equations shows that the solution checks. 

3x3x = 0 -2y - (+9y) = -11y 3x - 2y = 4 3x + 9y = 6 -11y = -2 y = 2 11 each term of second equation multiplied by 3 subtract 4-6=-2