In Example 7, change sin to cos. Data from Example 7 Find the rectangular equation of the rose r = 4sin 2. Using the trigonometric

In Example 7, change sin to cos.

Data from Example 7

Find the rectangular equation of the rose r = 4sin 2θ. Using the trigonometric identity sin2θ = 2sinθcosθ and Eqs. (21.41) and (21.42) leads to the solution:

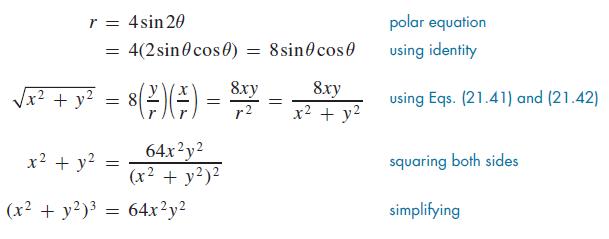
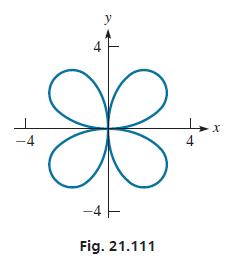
Plotting the graph of this equation from the rectangular equation would be complicated. However, as we will see in the next section, plotting this graph in polar coordinates is quite simple. The curve is shown in Fig. 21.111.

r = 4sin 20 x + y x + y = 4(2 sin cos 0) = 8 sin cos = = 8/ 8()() = 64xy (x + y) (x + y) = 64xy 8xy r2 = 8.xy x + y polar equation using identity using Eqs. (21.41) and (21.42) squaring both sides simplifying