All the information are in it

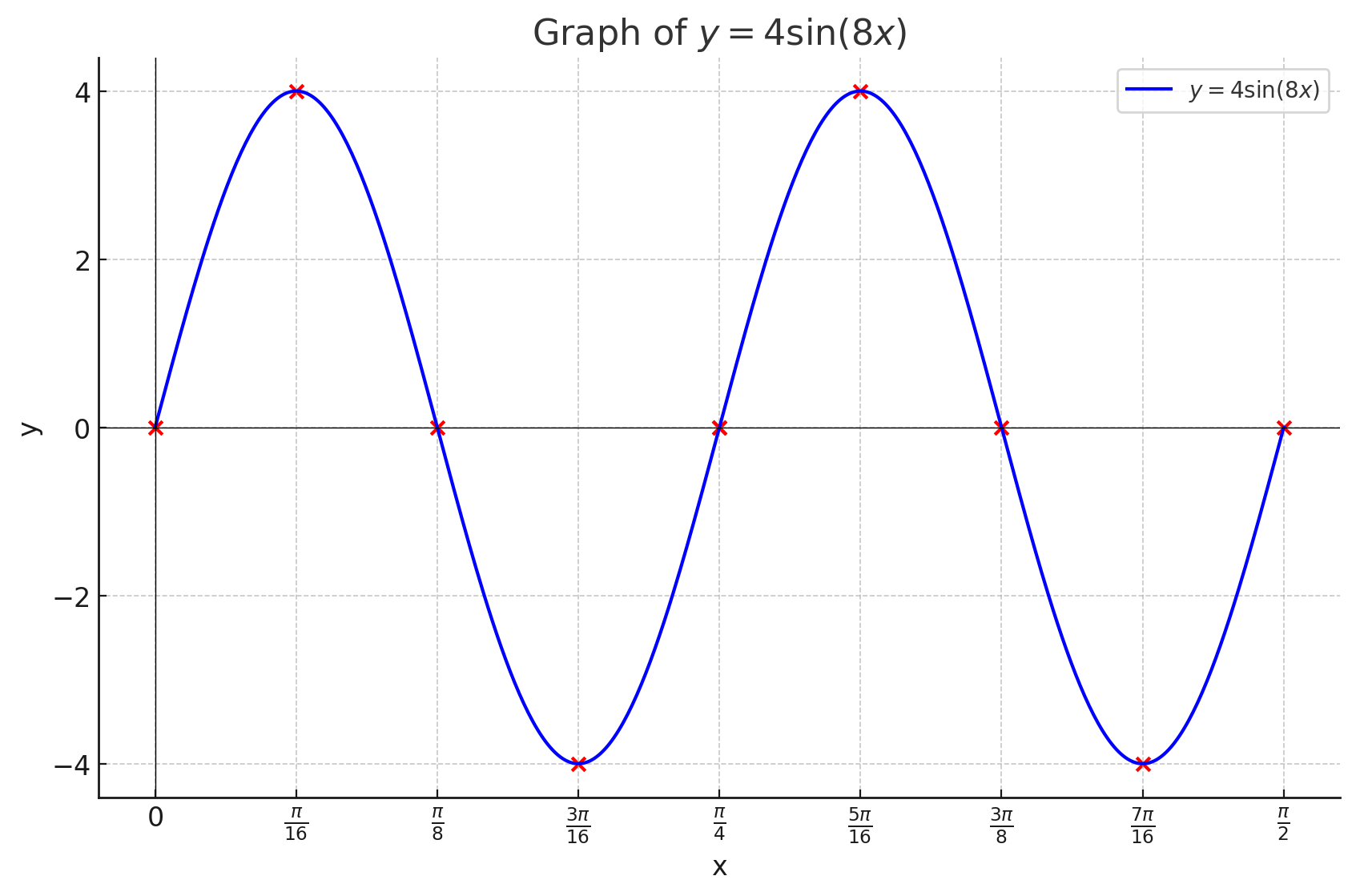
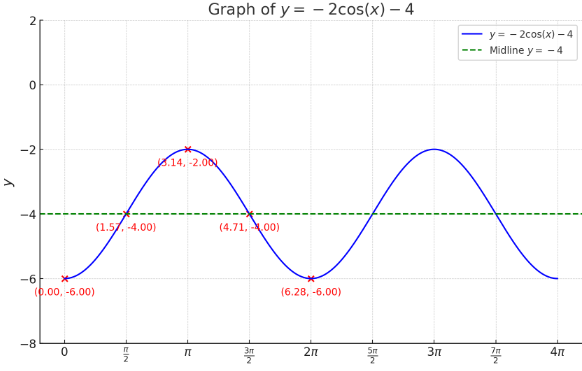
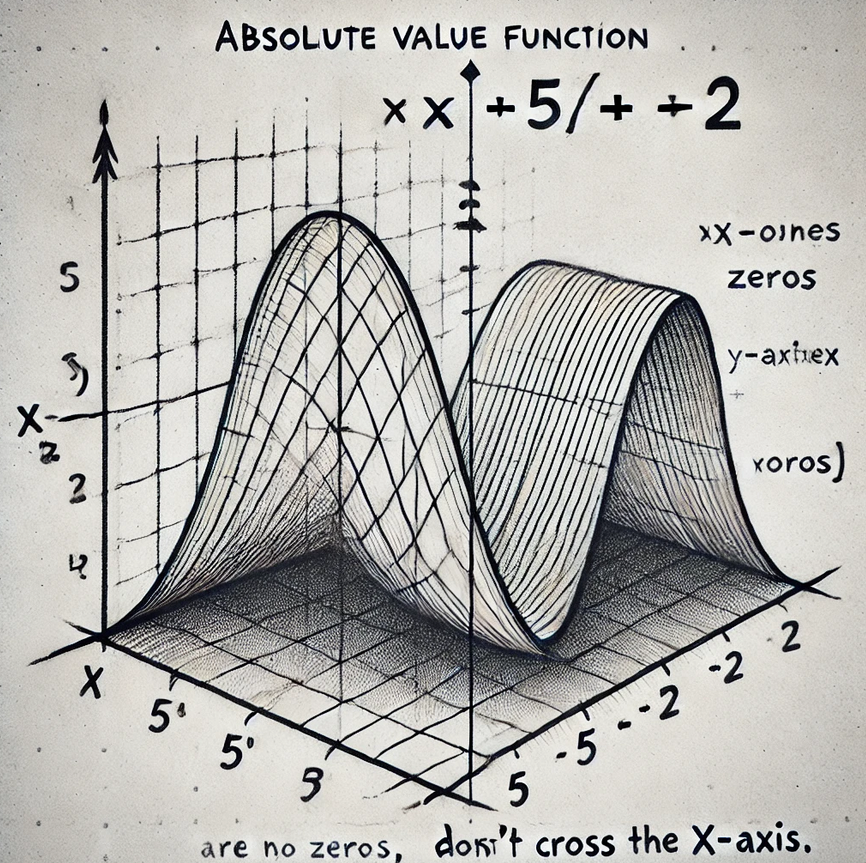
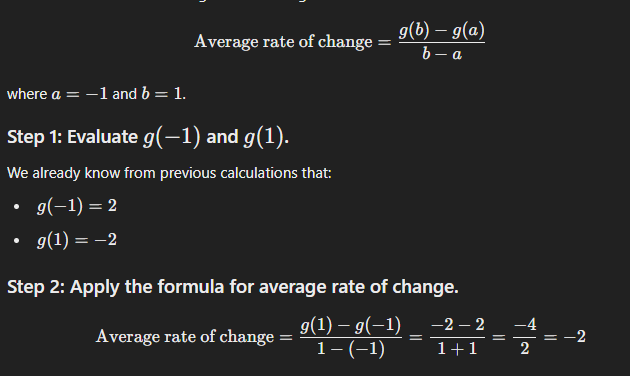
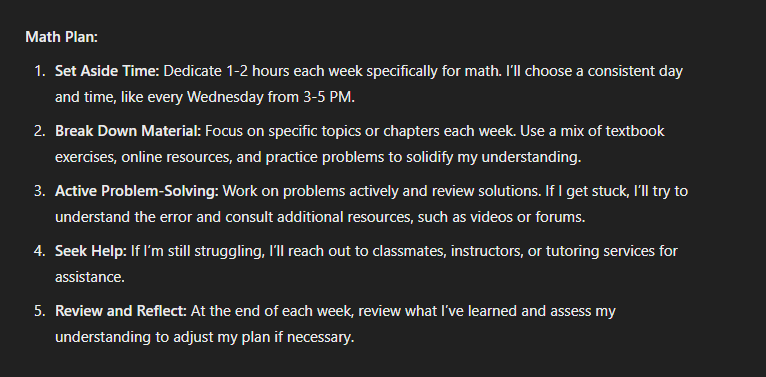
(i) g(x) = x?(x + 5)%(x 1)(x 4) (a) Degree: ; Leading coefficient: ; based on this the end behavior is: (b) the x-intercepts: X-intercept Multiplicity Bounce or cross? (c) the y-intercept: H W 2 5 (d) A graph based on everything from parts a c above: P E g E 2/2 Name Fall 2023 MAT 206 Homework 2.7 To receive full credit, all work must be shown and all problems must be attempted. 1.) Answer each part for the function g(x) = 6x3 29x? + 21x 4 a) List all the possible rational zeroes of g(x). b) Show that % is a zero of g(x). ) Find the remaining zeros of g(x). d) Complete the linear factorization of the function g(x). H.W 2.7 page 1/2 2.) Given: f(x) = x* x3 6x? a) Determine the end behavior of f(x). b) Use synthetic division to show that 2 is the zero of the given function. ) Find the remaining the zeros, multiplicity of each zero and state whether the graph crosses or touches the x-axis. c) Sketch the graph. HW 2.7 Page 2/2 Name Fall 2023 MAT 206 Homework 4.7 To receive full credit, all work must be shown and all problems must be attempted. Need to review this material first? Check out the dedicated Lesson 4.7 playlist! https://www.youtube.com/watch?v=GVLrrGT9aM8&list=PLDP6hC4Qvja118phyf-tg8pN2sS9MWOxd 1.) a) State the domain of the function. b) Find any vertical asymptotes and the coordinates of any holes. c) Find the horizontal asymptote, if one exists. d) Find the x- and y - intercepts. e) Describe the behavior of the function to the left and right of the vertical asymptote or find a few points around each asymptote. i.) g(x) = *-6 x+3 a) State the domain of the function. b) Find any vertical asymptotes and the coordinates of any holes. H.W 4.7 c) Find the horizontal asymptote, if one exists. Page 1/2 d) Find the x- and y - intercepts. e) Find a few points to the left and right of each asymptote. N -6 -4 -2 0 2 4 6 N -6ii.) f ( x ) = - 2x2+ 6x x2 + 2x - 3 a) State the domain of the function. b) Find any vertical asymptotes and the coordinates of any holes. H.W 4.7 c) Find the horizontal asymptote, if one exists. Page 2/2 d) Find the x- and y - intercepts. e) Find a few points to the left and right of each asymptote. N -6 -4 -2 0 2 4 6 -6Name Fall 2023 MAT 206 Homework 6.5 To receive full credit, all work must be shown and all problems must be attempted. Need to review this material first? Check out the dedicated Section 6.5 playlist! https://www.youtube.com/watch?v=Az7JJkiRo-4&list=PLDP6hC4Qvia2tOr4Ewz5Sre7dA-eouQxp 1.) Find all the relevant information and sketch a graph of each sine or cosine curve. For a and b, sketch two full periods. (a) y = 4 sin(8x) a = b = C = d =_ Amplitude: Period: Increments: Phase shift: Equation of midline: 5 key points for one period: X y H.W 6.5 Page 1/2(b) y = 2cos(x) 4 a= b= c= d= Amplitude: Period: Increments: Phase shift: Equation of midline: 5 key points for one period: (c) y=%c05(x%)+3 H.w 6.5 Amplitude: Period: Increments: Phase shift: Equation of midline: I age 2/2 5 key points for one period: No need to graph this one @ Name Fall 2023 MAT 206 Homework 6.7 To receive full credit, all work must be shown and all problems must be attempted. Need to review this material first? Check out the dedicated Section 6.7 playlist! https://www.youtube.com/watch?v=YXqBiodUWJM&list=PLDP6hC4Qvia1xEIB2iJbVPz09cLFjOFMq 1.) Put away your calculator. 2.) Is it away? 3.) Just to be safe, put your phone away too. 4.) Evaluate the expression without using a calculator. Give your answer in radians. a.) arccos b.) arcsin(1) c.) arctan(1) d.) tan-1 (-13 ) e.) sin-1(-7) f.) cos-1 (-42) 5.) Keep the calculator away. 6.) Use the properties of inverse trigonometric functions to evaluate the expression. a.) sin (arcsin ()) b.) arccos (cos (#)) c.) sin(arctan(V3)) d.) arccos (sin ") H.W 6.7 Page 1/1Name Date: MAT 206.5 Homework 7.1 To receive full credit, all work must be shown and all problems must be attempted. Need to review this material first? Check out the dedicated Section 7.1 playlist! https://www.youtube.com/watch?v=exZLGdqEbws&list=PLDP6hC4Qvia2egxqKBZ-ZMfKvbc5N3_GJ 1.) List the 6 reciprocal identities. sin 0 = csc 0 = cos 0 = sec 0 = tan 0 = cote = 2.) List the two quotient identities. tan 0 = cot 0 = 3.) List the 9 ways to write the Pythagorean Identities. (There are 3 but each can be written in 3 different ways.) These are the identities that you can apply to verifying trigonometric identities, in addition to other strategies (factoring/distributing/combining/etc.) 4.) Factor: csc2(0) - cos (0) . csc (0) 5.) Combine and simplify: sec(a) - 1 sec(a) + 1 H.w 7.1 page 1/2 6.) Verify the following identities. Be sure to show each step. a.) (1 - cos 0) (1 + cos 0) = sin2 06.) Verify the following identities. Be sure to show each step. a.) (1 - cos 0) (1 + cos 0) = sin2 0 b.) sec- a _ - + tan a tan a tan a H.w 7.1 page 2/2Name Date: MAT 206.5 Homework 7.2 To receive full credit, all work must be shown and all problems must be attempted. Need to review this material first? Check out the dedicated Section 7.2 playlist! https://www.youtube.com/watch?v=Ai-zolJwEqs&list=PLDP6hC4QvjaOTrx1K-kHyYipOKEzKJMII Verify the identity. Remember that you only want to manipulate ONE SIDE of the equation only. 1.) csex - sin x = cos x cotx 2.) cot B - cot B cos B = sin B cos B 3.) 1 - sin 0 cos e = sec 0 - tan 0 H.w 7.2 page 1/1Name Week 6 MAT 206 Group Quiz 6 Please do not use solvers/solving apps/solving websites. I want to see what you know & Question | is worth 5 points and question 2 is 15 points. Be sure to show all work!!! 1.) What is the remainder of the following division? (7x% + 6x* 9) =+ (x + 3) 2.) Find all zeros of the function f(x) = 4x* 12x% 19x + 12 by answering each part. (a) Use the Rational Zero Test to list the possible rational zeros for f{x). (b) Use synthetic division to show that 4 is fact one of the zeros of f(x) and that % is NOT a zero of fix). (c) Find the remaining zeros of f(x). Show all your work!! (d) Write the complete linear factorization of f(x). G - Q 6 Name Week 3, Fall 2024 MAT 206 Group Quiz 3 Show me what you know!!!!! Work with your classmates or on your own to answer these questions. Please do not use solvers/solving apps/solving websites. I want to see what you know Each question is worth 5 points. 1.) Given the function in the graph, answer the following questions. g(x) = x3 - 3x g(x ) a.) What are the domain and range of the function? Write your answer in interval notation. b.) State the intervals on which the function increasing or decreasing. c.) Identify all relative extrema of g(x). d.) Find the average rate-of-change from x = -1 to x = 1. G.Q3 Page 1/2i) The domain is (c0, ) and the range is [4, ). ii.) The zeros of the function are (-2, 0) and (1,0). iii) The y-intercept is (0, -4). iv.) The function increases on (0, ). The function decreases on (-2, 0). The function is constant on (eo, 2). v.) The function is neither even nor odd. vi.) Name your function & h(x)=|x-5|+2 Vertex: Zeros: 4.) Simplify the radical based on the rules for simplifying radicals in the Snippets from 3 notes. (a) V56a12p20 (b) Jli_s G.Q3 Page 2/2 Must post first. 1.) Write about one of the following: * Think of a time in your life when you persevered and achieved your goal. Tell us about it. * How can you apply a growth mindset in this precalculus course this fall? 1. We use linear equations all the time though we may not be aware of it! When is a time *outside of a math or science classroom that you have used a linear equation. **If you say never, you receive no credit.** For example, when you take a cab, there is an initial charge of $3, plus $0.70 per 1/5th mile. Therefore the cost of a cab is represented by: C=3+0.7/m where m is one- fifth of a mile. Post due 9/8 1. Hopefully you have formed some type of \"'math time\" each week. What is your math plan? What have you/will you do when you get stuck on the material? Post due 9/16 2. Respond to/send encouragement to at least two of your classmates' posts. 1.) The past three and a half years has been exceedingly challenging for many, if not all, of us. Share positive thing that happened to you, that you learned about yourself, or something good in the past 3.5 years. Post due 10/8 1. Find a graph of something *in the real world* that appears to have an exponential shape. You must cite your course!! Posts due 10/21 1. Since it is a holiday week* (Veteran's Day and also Election Day sort of counts!), let's create our own! If it were up to you, what National Holiday would you create? On what day would it be on? Due 11/11 \fGiven the function: EC 6 9(#) = a) Domain of the Function The domain of the function is all real numbers except where the denominator equals zero because division by zero is undefined. Set the denominator equal to zero and solve for c: #+3=0 Thus, the domain of g(x) is: Domain: {o ( R | x / -3} b) Vertical Asymptotes and Holes Vertical Asymptote: Vertical asymptotes occur where the denominator is zero and the numerator is not zero at the same point. Here, the denominator is + + 3. Since a = -3 makes the denominator zero, and the numerator - 6 is not zero at x = -3, there is a vertical asymptote at C= -3 Holes: Holes occur where both the numerator and denominator are zero at the same point, which does not apply in this case since c - 6 does not become zero when + + 3 does. Thus, there are no holes in the graph of g()- c) Horizontal Asymptote The horizontal asymptote is determined by comparing the degrees of the numerator and the denominator. The degree of the numerator (which is 1 for z) is equal to the degree of the denominator (which is also 1 for c)- When the degrees are equal, the horizontal asymptote is given by the ratio of the leading coefficients of the numerator and the denominator. Here, both coefficients are 1, so the horizontal asymptote is: HId) X- and Y-Intercepts X-Intercept The x-intercepts occur where g () = 0. For a fraction, the numerator must be zero for the function to be zero. Set the numerator equal to zero: 1-6=0 =6 Thus, the x-intercept is (6, 0). Y-Intercept: The y-intercept occurs where = = 0. Substitute + = 0 into g (x): 0- 6 -6 9(0) = = -2 0+3 3 Thus, the y-intercept is (0, -2). e) Points to the Left and Right of Each Asymptote We already know there is a vertical asymptote at a = -3. Let's find some points to the left and right of this asymptote. Choose x = -4 and x = -5 to the left of r = -3. Choose x = -2 and = = -1 to the right of * = -3. Now, we'll calculate g(a ) for these values. -4-6 g(-4) = = 10 -4+3 -1 -5-6 9(-5) = - 5.5 -5+3 9(-2) = 6 -2+3 1 9(-1) = -1- 6 -7 -3.5 -1+3 21. Amplitude: The amplitude A is the coefficient in front of the sine function, which is 4. Amplitude: A = 4 2. Period: The period I of a sine or cosine function is given by the formula: T = B Where B is the coefficient of x inside the sine function. Here, B = 8. T = 3. Phase Shift: The phase shift o is given by. Phase Shift = Where C is the horizontal shift (inside the function). In this case, since y = 4 sin(8x) does not have a C term, there is no phase shift Phase Shift: $ = 0 4. Vertical Shift (Midline): The vertical shift D is the constant term added to the function. Since there is no vertical shift term, the midline is at y = Q. Equation of the Midline: y = 05. Increments: To plot the sine curve, we typically divide the period into 4 equal parts [increments). Period 71 /4 Increment = 16 6.5 Key Points for One Period: For a sine function y = Asin(Bx), the key points occur at (0, 0) , jed, A). (Period, o). ( aPeriod, -A) , (Period, 0) Using our values: EG y 7. Sketching Two Full Periods Since one period is I. two periods will be . The key points for the second period will just continue with the same pattern. Points for the second period: 4\f1. Amplitude: * The amplitude a is the coefficient of the cosine function, which determines the height of the wave from the midline. + Amplitude = | 2| = 2. 2. Period: * The period of the cosine function is determined by the formula Period = .E_;r where b is the coefficient of @ inside the cosine function. s Here, b = 1, so the Period = \"1' = 2. 3. Phase Shift: * The phase shift is calculated as 4-. Since there is no honizontal shift {i.e, no term), the Phase ST A 4. Equation of Midline: * The midline is determined by the constant term d, which shifts the graph vertically. * Equation of Midline = y = 4. 5. Increments: s The increments for key points on the graph can be calculated by dividing the period by 4: oot R S 4 4 - 6.5 Key Points for One Period: Now, let's calculate the 5 key points over one period: Start with : = 0: y(0) = -2 cos(0) - 4= -2(1) -4= -2-4=-6 Next, I = 5: -4= -2(0) -4=-4 Then, I = 7: y(7) = -2 cos(7) - 4= -2(-1) -4=2-4=-2 . Then, 1 = M; 3TT y = -2 cos 2 -4= -2(0)-4=-4 Finally, I = 27: y(27) = -2 cos(27) - 4= -2(1) -4=-2-4=-6 Summary of Key Points: y D -6 -4 -2 -4 2 TT -61. Amplitude The amplitude is the coefficient in front of the cosine function, which determines the vertical stretch or compression. For this function: Amplitude = = 2. Period The period of a cosine function y = A cos(BI - C) + D is given by: Period = B In this case, B = 1, so the period is: Period = = 2T 3. Increments The increments (step between key points) for one period can be found by dividing the period by 4: Period 271 Increments = 4 4. Phase Shift The phase shift is determined by the expression : - I inside the cosine function. The phase shift is: Phase Shift = B Since I is positive, the graph shifts to the right by I.5. Equation of the Midline The midline is the horizontal line that the function oscillates around, given by the constant D in the equation: Midline = y = 3 6. 5 Key Points for One Period To find the key points, we start from the phase shift and add the increments. Let's list the x values: 1. Start = = - 2. First increment: c = = + 3. Second increment = = 4. Third increment: 1 = = + = 5. End: = = Corresponding y values: Plugging these x values into the function: 1. = = 1 y = = 008 (0) + 3 = }(1) +3 =3.5 2 0 = 7. y = 1 008 (7) +3 =1(0) +3 =3 3. = = 4. y = 1 008 (#) +3=1(-1)+3=2.5 4. = = 4 y =1008 (#) +3=}(0) +3=3 5. = = H. y = 1 008 (27) + 3 = (1) +3 =3.5 Summary of Key Points: y 3.5 3 2.5 3 3.5a) Domain of the Function The domain of a function is the set of all possible values of a for which the function is defined. Since this is a rational function, it will be undefined where the denominator is zero. 1. Find the values of a that make the denominator zero: I' + 2x - 3=0 2. Solve the quadratic equation: (x +3)(x - 1) =0 So, x = -3 and x = 1 are the values that make the denominator zero. 3. Domain: The function is defined for all a except where the denominator is zero. Domain: F E (-Do, -3) U (-3, 1) U (1, 00) b) Vertical Asymptotes and Holes Vertical asymptotes occur where the denominator is zero and the numerator is not zero at those points. Holes occur where both the numerator and the denominator are zero at the same point. 1. Factorize the numerator and denominator. Numerator: 2r' + 6: = 2x(x + 3) Denominator: x' + 2x - 3 = (x +3)(x - 1) 2. Simplify the function: f(C) = 2x ( # + 3) ( + 3)(x - 1) Simplifying, we get: f(=)=1' for x * -3 3. Identify vertical asymptotes: Vertical asymptotes occur at a = 1 since the function is undefined there and doesn't cancel out. 4. Identify holes: A hole occurs at + = -3 because the factor ( + 3) cancels out in both the numerator and the denominator. Coordinates of the hole: Substitute x = -3 into the simplified function: 2(-3) f(-3) = -3- So, there is a hole at ( -3, _).c) Horizontal Asymptote Horizontal asymptotes are determined by comparing the degrees of the polynomial in the numerator and denominator. 1. Degrees of numerator and denominator. The degree of the numerator 2:x* is 2. The degree of the denominator c" is 2. 2. Since the degrees are equal: The horizontal asymptote is determined by the ratio of the leading coefficients: Horizontal asymptote: y = HIN = 2 d) X and Y Intercepts 1. X-intercepts: These occur where the numerator is zero. 2x(x + 3) = 0 c = 0 and + = -3 are solutions. But * = -3 corresponds to the hole, so the only valid x-intercept is = = 0. X-intercept: (0, 0) 2. Y-intercept: This occurs where = = 0. 2(0) f(0) = 0-1 Y-intercept: (0, 0) e) Points to the Left and Right of Each Asymptote To sketch the graph more accurately, let's find a few points to the left and right of the vertical asymptote at = = 1. 1. Left of : = 1 (e.g. = = 0.5): 2(0.5) 1 f(0.5) = 0.5 - 1 0.5 -2 Point: (0.5, -2) 2. Right of * = 1 (eg, $ = 1.5): 3 f (1.5) = 2(1.5) 1.5 - 1 =6 0.5 Point: (1.5, 6)a) arccos(undefined) Since there's no value provided inside the parentheses for arccos, this part seems incomplete. Typically. arccos( ) gives the angle 0 such that cos (0) = x, where a must be in the range [ 1, 1]. If you have a specific value in mind, let me know, and I'll evaluate it! b) arcsin(1) The arcain (x) function gives the angle & such that sin (0) = r. For arcsin (1). we need to find @ such that sin (8) = 1. The sine function equals 1 at 0 = = radians. Answer: arcsin (1) = = radians. c) arctan(1) The arctan (x ) function gives the angle 0 such that tan (0) = r. For arctan(1). we need to find & such that tan (0) = 1. The tangent function equals 1 at d = = radians. Answer: arctan (1) = = radians. d) arctan Va The arctan (r) function gives the angle 0 such that tan (0) = . For arctan ( - ). we need to find & such that tan (0) = - 42 The tangent function equals - at 0 = -= radians. Answer: arctan = - radians. e) arcsin(-7) The arcsin (x) function gives the angle 0 such that sin (0) = . However, the domain of arcsin (x) is restricted to [-1, 1]. and -7 is outside this range. Therefore, arcain(-7) is undefined. Answer: arcsin(-7) is undefined. f) arccos The arccos(e ) function gives the angle & such that cos (0) = E. For arccos ( - ). we need to find @ such that cos(0) = _1/2 The cosine function equals - at 0 = " radians. Answer: arccos 42 radians.a) sin(arcsin ()) The arcain (x) function retums an angle o such that sin (0) = . Here, arcsin (* ) is the angle @ such that sin (0) = = Applying the sine function to this angle simply returns the original value. Answer: sin(arcsin ()) = 3- b) arccos(cos(4)) The arccos(a ) function returns an angle d such that cos (0 ) = E. Here, cos(1 ) = , so arccos (cos(#)) asks for the angle @ such that cos (0) = $2. Since : is within the range of the arceos function (which is [0, x]). we simply have: Answer: arccos (cos({ )) = 1 c) sin (arctan(3)) The arctan (c) function returns an angle 0 such that tan (0) = F. Here, arctan( v3) is the angle 0 such that tan (0) = v3. The angle & for which tan (0) = v3 is ; radians. Now, sin (G) = 42. Answer: sin (arctan(v3)) = 4. d) arccos(sin ()) First, calculate sin (; ): sin ( *) = 42 Now, we need to evaluate arccos The arocos(a ) function returns an angle d such that cos (0) = E. The angle { for which cos(0) = 1 is 0 = = radians. Answer: arccos (sin (= ) ) = =-1) List the 6 Reciprocal Identities The reciprocal identities relate the basic trigonometric functions to their reciprocals. Here they are: sin (0) = CBC(8 ) = csc(8) sin(8) cos(0) = Soc(0 ) = sec(8 ) 1 1 tan (0) = cot(0) = cot (0) tan (8) 2) List the Two Quotient Identities The quotient identities express tangent and cotangent in terms of sine and cosine: tan (0) = sin(8) cos(8) cos (8) cot (0) = sin (8) 3) List the 9 Ways to Write the Pythagorean Identities There are three main Pythagorean identities, each of which can be rearranged in three different ways: 1. First Pythagorean Identity: sin'(0) + cos (0) = 1 Rearranged forms: sin (0) =1 - cos' (0) cos'(0) = 1 - sin' (0) 2. Second Pythagorean Identity: 1 + tan (0) = sec'(0) Rearranged forms: tan' (0) = sec'(0) - 1 sec' (0) = 1 + tan'(0) 3. Third Pythagorean Identity: 1 + cot (0) = cac(0) Rearranged forms: cot'(0) = cac'(0) - 1 cac'(0) = 1 + cot' (0)4) Factor: csc-(0) - cos(0) . csc(0) Let's factor the expression: cac' (0) - cos(0) - cac(0) Notice that cac(0) is a common factor. esc(8) (csc(8) - cos(@)) Answer: cac(8) (csc(0) - cos (0)) 5) Combine and Simplify: sec(a)-1- sec[a)+1 Let's combine the two fractions: sec(o) - 1 sec(a) + 1 Find a common denominator. (sec(a) + 1) - (sec(a) - 1) (sec(a) - 1)(sec(a) +1) Simplify the numerator. sec(a) + 1 - sec(a) + 1 2 (sec(a) - 1) (sec(a) + 1) sec' (a) - 1 Using the Pythagorean identity sec- (a) - 1 = tan' (a): 2 tan (a) Simplify further. 2 2 tan'(a) tan'(a) = 2 . cot (a) Answer: 2 . cot- (a)a) Verify (1 - cos(0)) (1 + cos(0)) = sin?(0) We start by expanding the left side of the equation: (1 - cos(0)) (1 + cos(0)) This is a difference of squares, which follows the identity (a - b) (a + b) = a - 63. Here, a = 1 and b = cos (8): 12 - cos' (0) =1 - cos (0) Now, recall the Pythagorean identity: sin (0) =1 - cos' (0) Thus: 1 - cos (0) = sin' (0) So we have: (1 - cos(0)) (1 + cos(0)) = sin' (0) The identity is verified. b) Verify sec (@) tanja) = tan(a + tan(a) We'll start by simplifying the left side of the equation. Left Side: Sec (C) tan(a) Recall that sec(c) = air and tan(a) = (aj- Al shoal Also, sec' (o) = 1 + tan' (a) from the Pythagorean identity. So: sec-(a) 1 + tan'(a) tan(o) tan(o) We can break this into two fractions: 1 + tan (a) tan (o) tan(o) tan(o) tan(a) Simplify the second fraction: 1 tan' (a) + tan(a) tan(a) tan(c) tan(a) This is exactly the right side of the equation. The identity is verified.1) Verify csc(z) sin(z) = cos(z) cot(z) Let's start by manipulating the left side of the equation: R T Y| Recall that ese(z) = and cot(z) = Recognizing that E' e R B This matches the right side of the equation. The identity is verified. 2) Verify cot(8) - cot(B) cos(8) = sin(B) cos(B) Let's start by manipulating the left side of the equation: cot (8) - cot (B) cos' (A) Factor out cot (8): cot (8) (1 - cos' (8)) Use the Pythagorean identity 1 - cos' (8) = sin(8): cot (8) . sin (8) Recall that cot (8) = cos(8) . sin'(8) sin(8) Simplify the expression: cos (8) - sin (8) This matches the right side of the equation. The identity is verified.1 - sin(0) cos(8) = sec(0) - tan(0) We'll start by manipulating the right side of the equation to see if we can transform it into the left side. Right Side: sec(0) - tan(0) Recall the definitions of secant and tangent in terms of sine and cosine: 1 sin (8) Soc (0 ) = tan(0) = cos ( 6 ) Substitute these into the right side: sec (8) - tan(0) = sin (0) cos(8 cos[ d ) Combine the fractions over a common denominator. 1 - sin(0) cos (0) This matches the left side of the equation exactly: 1 - sin(0) 1 - sin(8) cos (8 ) cos () The identity is verified.Characteristics Breakdown: 1. Domain: (-oo, co) (The function is defined for all real numbers.) 2. Range: [-4, oo) [The lowest value the function can reach is -4) 3. Zeros: (-2, 0) and (1, 0) (The function crosses the x-axis at these points.) 4. Y-intercept: (0, -4) (The function crosses the y-axis at (0, -4)) 5. Behavior. Decreases on (-Do, -2) and on (-2, 0). Constant on (-oo, -2)- Increases on (0, oo). 6. Neither even nor odd: This means the function does not have symmetry about the y-axis or the origin. Steps to Draw the Function: 1. Plot the points: Plot zeros at (-2, 0) and (1, 0). Plot the y-intercept at (0, -4). 2. Constant behavior on (-co, -2): Draw a horizontal line on the interval (-oo, -2) at a certain value. It should be flat. 3. Decreasing behavior from (-2, 0): From (-2, 0), the function should decrease to the point (0, -4). 4. Increasing behavior on (0, co): From the point (0, -4). the function should rise to infinity as x moves towards infinity. 5. Smooth transition: Ensure the function transitions smoothly between these behaviors without sharp turns, which means using curves to connect the points and behavior.Understanding the Transformation: he given function s a transformation of the basic absolute value function :r| 1. Horizontal Shift: b inside the absolute value shifts the graph & units to the right 2. Vertical Shift: The 42 outside the absolute value shifts the graph 2 units up. ertex: he vertex of the basic absolute value function y = 2| is at [0, 0). After applying the ransformations: # The graph shifts 5 units to the right, so the -coordinate of the vertex becomes. &. The graph shifts 2 units up, o0 the y-coordinate of the vertex becomes 2. S || o find the zeros (where the function crosses the x-axis), set i I::.'} = |.r 5||E: Subtract 2 from both sides: b| =-2 Howvever, since the absolute value |.r 5| is always non-negative. it cannot equal 2. Therefore, he equation has no real solutions. [Zeros: There are no zeros for this function =1 o sketch the graph: 1. Start with the basic graph of :r| 2 Shift the vertex to (5, 2). 3. Plot the vertex (5, 2) on the graph. 4. Draw the V-shaped graph opening upwards from the vertex. Since there is no change in the e (the coefficient of ( 5| iz 1), the graph will have a 45" angle on each side. his gives you a graph that starts at (5, 2) and moves upwards in both directions. ABSOLUTE VALUE FUNCTION XX + 5/+ +2 xX-oines 5 + zeros y-axhex X- xoros) - 5 - -2 2 2 X 5' 5 3 5 are no zeros, don't cross the X-axis.(a) Domain and Range Domain: The domain of a polynomial function is always all real numbers since there are no restrictions like square roots or denominators. Domain: (o0, c0) Range: To determine the range of the cubic function, let's analyze the behavior c:fg{:l:}. Since this is a cubic function, it will extend to infinity as & + o0 and to negative infinity as # + o0. Hence, the range is also all real numbers. Range: (oo0, 00) (b) Intervals of Increase and Decrease To find the intervals on which the function is increasing or decreasing, we need to compute the first derivative g'(z) and determine where it's positive or negative. Find the first derivative '(z): IO SR F Find the critical points: Critical points occur where g'(z) = 0: P Y =1 = = =+1. So, the critical points arez = 1 and z = 1. Test the sign of g'(z) in the intervals: 1. Interval (oo, 1): Pick a test point, say & = 2: g(2)=3(-2)>-3=3(4)-3=12-3=9>0. So, g'(z) > 0 on (oo, 1). The function is increasing on this interval. . Interval (1, 1): Pick a test point, say z = (: g'(0) =3(0)>-3=-30. So, g'(z) > 0 on (1, 00). The function is increasing on this interval. Increasing intervals: (oo, 1) U (1, c0) Decreasing interval: (1,1) (c) Relative Extrema To identify the relative extrema, we analyze the critical points where the function changes from increasing to decreasing or vice versa. At x = 1, the function changes from increasing to decreasing, so there is a relative maximum atx = 1. At z = 1, the function changes from decreasing to increasing, so there is a relative minimum at =1 Find the values of the relative extrema: Relative maximum at > = -1: g(-1) = (-1)8 - 3(-1) =-1+3 =2. So, the relative maximum is (-1, 2). Relative minimum at c = 1: g(1) = (1)3 - 3(1) =1-3=-2. So, the relative minimum is (1, -2). Final Answers: (a) Domain and Range: Domain: (-co, co), Range: (-00, 00). (b) Intervals of increase and decrease: Increasing: (-00, -1) U (1, co), Decreasing: (-1, 1). (c) Relative extrema: Relative maximum at (-1, 2), Relative minimum at (1, -2).Average rate of change = g(b) - g(a) b- a where a = -1 and b = 1. Step 1: Evaluate g(-1) and g(1). We already know from previous calculations that; . g(-1) = 2 . g(1) = -2 Step 2: Apply the formula for average rate of change. Average rate of change = g(1) - g(-1) 2-2 = = -2 1- (-1) 1+1 2Step 1: Set up the synthetic division We divide Tz3 4+ 622 9 by + 3. In synthetic division, we use the root of + 3, which is 3. The coefficients of the polynomial 7z* + 6z2 + 0z 9 are: 7, 6,0, 9. Step 2: Perform the synthetic division V) 9 21 45 135 Here's how it works: Bring down the first coefficient 7. Multiply 7 by 3, which gives 21. Add it to the next coefficient 6 to get 15. Multiply 15 by 3, which gives 45. Add it to the next coefficient 0 to get 45. Multiply 45 by 3, which gives 135. Add it to the next coefficient 9 to get 144. Step 3: Identify the quotient and remainder The quotient is the polynomial formed by the numbers in the bottom row {(ignoring the last number): 7z% 15z + 45 The last number in the row is the remainder: Remainder = 144. Final Answer: The remainder of the division of Tz + 62> 9byz + 3 is . (a) Use the Rational Zero Test to list the possible rational zeros for f(.l:) The Rational Zero Test states that the possible rational zeros are the ratios of the factors of the constant term (12) to the factors of the leading coefficient (4). Factorsof 12: +1, 42, +3, +4, +6, +12 Factorsof4: +1,+2, +4 Thus, the possible rational zeros are the ratios of the factors of 12 divided by the factors of 4. The possible rational zeros are: 1 " R S =Y :I:g,:l:, +12. (b) Use synthetic division to show that 4 is a zero and that -3 is NOT a zero of o) Test = 4 using synthetic division: Coefficients of f(z) = 4a 1222 + 19z + 12 are 4, 12,19, 12. Set up synthetic division for 2 = 4: 414 -12 19 12 16 16 140 4 35 152 The remainder is 152, so = 4 is NOT a zero of f(.l] (a) Rational Zero Test Recap We listed the possible rational zeros for f(z): 1 L3 R N Y :I:g i N (b) Finding = 4 as a Zero via Synthetic Division We previously tested & = 4 but found that it did NOT work as a zero of the function. Let's retry with a known correct root (e.g., = 4) or another candidate from the Rational Zero Test. Synthetic Division for z = 4: We will run the process accurately to confirm if there was an issue in interpretation. Using Synthetic Division Correctly: Let's test # = 1 now, comrectly, or any Applying a Growth Mindset in Precalculus As | prepare for precalculus this fall, | recognize the importance of a growth mindsetthe belief that intelligence and abilities can develop with effort and perseverance. In the past, |'ve faced challenging subjects that initially seemed overwhelming, but through persistence and a willingness to embrace mistakes as learning opportunities, | saw significant progress. Precalculus, with its complex concepts and abstract thinking, is no different. | know there will be times when I'll struggle with a particular function, theorem, or proof, but instead of seeing those struggles as barriers, | will view them as steps toward mastery. Each mistake will be a chance to deepen my understanding, and I'll remind myself that every concept | grasp brings me closer to success. By adopting a growth mindset, | will focus on consistent effort, ask questions when needed, and trust that even the most difficult problems can be solved with patience and determination. This approach will not only help me thrive in precalculus but also build resilience that | can apply to other areas of [} A time I used a linear equation outside of a math or science classroom was when I was budgeting for a personal project. I wanted to redecorate my room, and I needed to calculate the total cost for supplies like paint, shelves, and decorations. I knew that each can of paint was $25, and every shelf cost $15. I needed 3 cans of paint and 4 shelves. I created a linear equation to determine the total cost: C = 25p + 15s where p is the number of cans of paint and s is the number of shelves. Plugging in the numbers, I got: C = 25(3) + 15(4) = 75 + 60 = 135. The total cost was $135. This was a practical use of linear equations in my daily life to help me budget efficiently.Math Plan: 1B Set Aside Time: Dedicate 1-2 hours each week specifically for math. I'll choose a consistent day and time, like every Wednesday from 3-5 PM. 2. Break Down Material: Focus on specific topics or chapters each week. Use a mix of textbook exercises, online resources, and practice problems to solidify my understanding. 3. Active Problem-Solving: Work on problems actively and review solutions. If | get stuck, I'll try to understand the error and consult additional resources, such as videos or forums. . Seek Help: If I'm still struggling, I'll reach out to classmates, instructors, or tutoring services for assistance. . Review and Reflect: At the end of each week, review what I've learned and assess my understanding to adjust my plan if necessary. Encouragement Responses: L To Classmate A: \"| really admire how you've been tackling these challenges head-on. Your dedication is inspiring, and I'm confident that with your persistence, you'll master the materal in no time. Keep up the great work!\" 2. To Classmate B: "It's impressive to see how you've adapted to the difficulties over the past few months. Your positive attitude and resilience are truly commendable. Remember, every challenge is a step towards growth. You've got this!\