Make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 10, change the numerator to 2x⁴ − 32x² and then simplify.

Data from Example 10

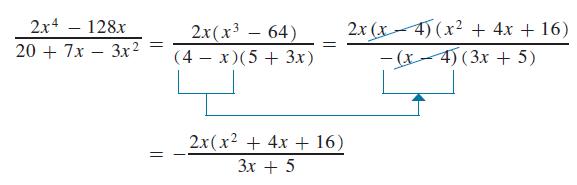
Again, the factor 4 − x has been replaced by the equivalent expression −(x − 4). This allows us to recognize the common factor of x − 4. Also, note that the order of the terms of the factor 5 + 3x was changed in writing the third fraction. This was done only to write the terms in the more standard form with the x- term first. However, because both terms are positive, it is simply an application of the commutative law of addition, and the factor itself is not actually changed.

2x4 - 128x 207x3x = || 2x(x - 64) (4x)(5 + 3x) = 2x(x + 4x + 16) 3x + 5 2x (x4) (x + 4x + 16) -(x-4) (3x + 5)