Solve the resulting triangles if the given changes are made in the indicated examples of this section.

In Example 4, solve the triangle if the value of b is changed to 70.0.

Data from Example 4

Solve the triangle with the following given parts: a = 40.0, b = 60.0, and A = 30.0°. First, make a good scale drawing [Fig. 9.56(a)] by drawing angle A and measuring off 60 for b. This will more clearly show that side a = 40.0 will intersect side c at either position B or B'. This means there are two triangles that satisfy the given values. Using the law of sines, we solve the case for which B is an acute angle:

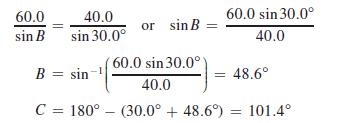
Therefore, B = 48.6° and C = 101.4°. Using the law of sines again to find c, we have

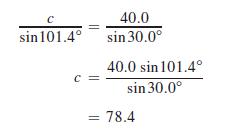
Thus, B = 48.6°,C = 101.4°, and c = 78.4. See Fig. 9.56(b).

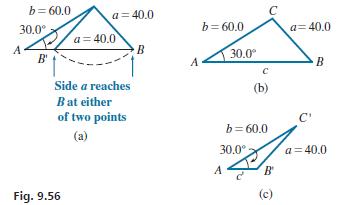
The other solution is the case in which B', opposite side b, is an obtuse angle. Therefore,

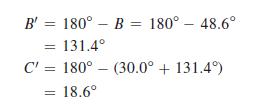
Using the law of sines to find c', we have

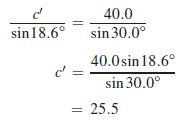
This means that the second solution is B' = 131.4°,C' = 18.6°, and c' = 25.5. See Fig. 9.56(c).

60.0 sin B 40.0 sin 30.0 or sin B 60.0 sin 30.0 40.0 60.0 sin 30.0 B = sin 40.0 C = 180 (30.0 +48.6) = 101.4 = 48.6