Solve the resulting triangles if the given changes are made in the indicated examples of this section.

In Example 1, solve the triangle if the value of C is changed to 145°.

Data from Example 1

Solve the triangle with a = 45.0, b = 67.0, and C = 35.0°. See Fig. 9.69. Because angle C is known, first solve for side c, using the law of cosines in the form c² = a² + b² − 2ab cos C. Substituting, we have

Now we will use the law of sines to find angle A (the smaller remaining angle).

Angle B can be found by using the fact that the sum of the angles is 180°: B = 180° − 35.0° − 40.6° = 104.4°. Therefore, c = 39.7, A = 40.6°, and B = 104.4°. After finding side c, solving for angle B rather than angle A, the calculator would show B = 75.5°. Then, when subtracting the sum of angles B and C from 180°, we would get A = 69.5°. Although this appears to be correct, it is not.

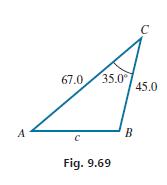
unknown side opposite known angle c= 45.0 + 67.0 2(45.0) (67.0)cos 35.0 c = 45.0 + 67.0 2(45.0) (67.0)cos 35.0 -known sides 39.7