From the approximation which holds for large n, deduce an expression for the log-likelihood L(px, y) and hence show that the maximum likelihood occurs when

From the approximation

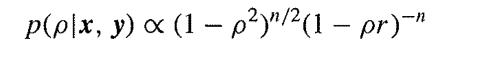
which holds for large n, deduce an expression for the log-likelihood L(pΙx, y) and hence show that the maximum likelihood occurs when ρ = r. An approximation to the information can now be made by replacing r by ρ in the second derivative of the likelihood, since ρ is near r with high probability. Show that this approximation suggests a prior density of the form

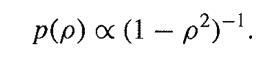
p(p\x, y) x (1 - p)/(1 pr)-n