Suppose that the density function p(xl) is defined as follows for x = 1, 2, 3, ... and = 1, 2, 3, .... If

Suppose that the density function p(xlθ) is defined as follows for x = 1, 2, 3, ... and θ = 1, 2, 3, .... If θ is even, then

Show that, for any x the data intuitively give equal support to the three possible values of θ compatible with that observation, and hence that on likelihood grounds any of the three would be a suitable estimate. Consider, therefore, the three possible estimators d₁, d₂ and d₃ corresponding to the smallest, middle and largest possible θ. Show that

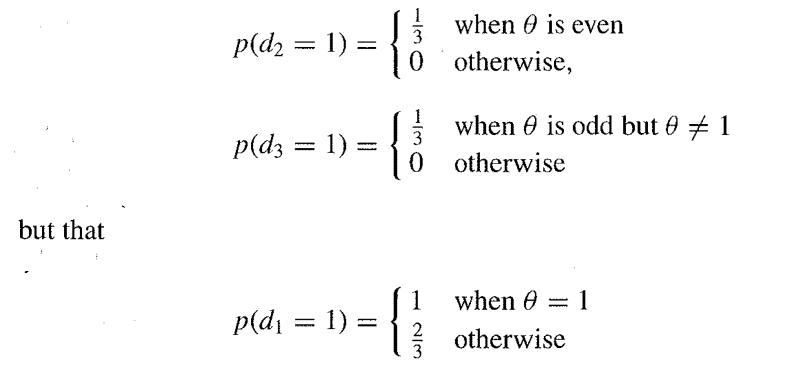Does this apparent discrepancy cause any problems for a Bayesian analysis ( due to G. Monette and D. A. S. Fraser)? 

p(x|0) = if 0 is odd but 01, then p(x|0) while if 0 = 1 then p(x|0) = - {} 0 otherwise 3 0 if x = 0/2, 20 or 20 + 1 {} if x = (0-1)/2, 20 or 20 + 1 otherwise if x = 0, 20 or 20 + 1 0 otherwise.