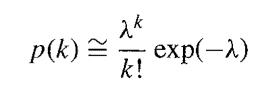
Suppose that k B(n,) where n is large and is small but n has an intermediate value Use the exponential limit ( 1 x ) n e x to show that P(k 0) e and P(k I) e Extend this result to show that k is such that that is, k is approximately distributed as a Poisson variable of mean p(k) exp( 2) 2k k ...

Given k follows a binomial distribution with parameters n and such that n is large T is small and n ...

Suppose that k ~ B(n,) where n is large and is small but n =

Question:

Suppose that k ~ B(n,π) where n is large and π is small but nπ = λ has an intermediate value. Use the exponential limit ( 1 + x )ⁿ → e^x to show that P(k = 0) ≌ e^-^λand P(k = I) ≌ λe^-^λ. Extend this result to show that k is such that

p(k)= exp(-) 2k k!