Suppose that m and n have independent Poisson distributions of means and , respectively (see question

Suppose that m and n have independent Poisson distributions of means λ and µ, respectively (see question 6) and that k = m + n.

 

(b) Generalize by showing that k has a Poisson distribution of mean λ + µ. 

(c) Show that conditional on k, the distribution of m is binomial of index k and parameter λ / (λ+ µ,).

Question 6.

Suppose that k ~ B(n,π) where n is large and π is small but n π  = λ has an intermediate value. Use the exponential limit (1 + x )ⁿ → e^x to show that P(k = 0) ≌ e^-λ and P(k = I) ≌  λe^-λ . Extend this result to show that k is such that 

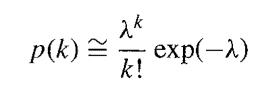
that is, k is approximately distributed as a Poisson variable of mean λ.

Transcribed Image Text:

(a) Show that P(k = 0) = e¯(^+μ) and P(k = 1) = (λ + µ)e¯(^+µ).