The observed Intel monthly returns for 2004 (the first comparing January 2004 with December 2003) are \(-0.047,-0.042,-0.069,-0.054,0.112,-0.033,-0.117\), \(-0.125,-0.058,0.109,0.007\), and 0.045. Compare the models in Example 6.11 in terms of their out-of-sample predictive performance for these future 12 observations.

Data from Example 6.11

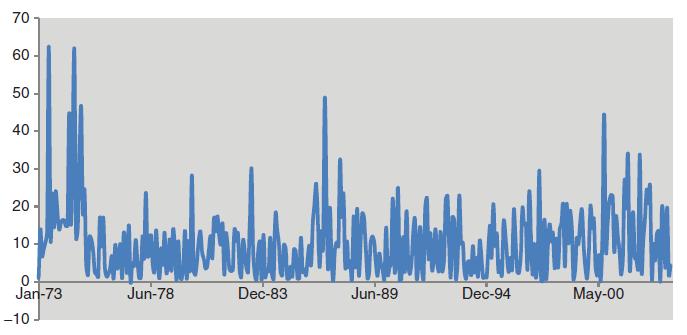
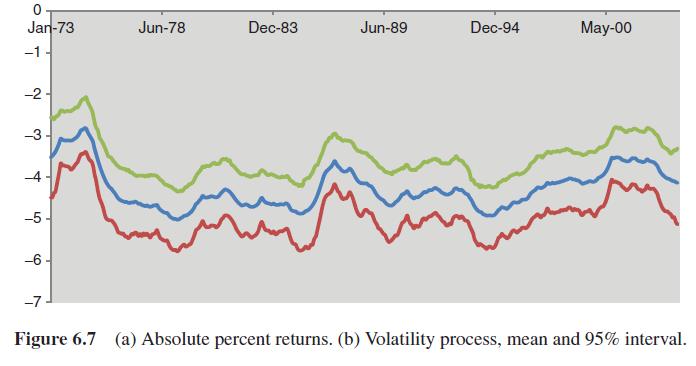
Let returns be defined as r = S/S-1 -1 for monthly Intel stock prices S, from January 1973 through to December 2003 (T = 372). Then consider log returns Y = log(r, + 1), centred to have average zero, y = Y-Y. The first three modeling options involve simple SV, ARCH and GARCH models. Thus as a first option, consider the autoregressive stochastic volatility (ARSV) model with y = exp(/2)u, K = + (K - ) + n where u ~ N(0, 1), n, ~N(0, 0) and || < 1. The prior on follows Meyer and Yu (2000), with * Be (20, 1.5), and then = 2* - 1. The second half of a two chain run of 10,000 iterations provides posterior mean (and 95% CRI) for of 0.94 (0.89, 0.98), with LPML of 245 and DIC of -494. The second option is an ARCH(1) model, with y = h u = 1-1 = @ 1-1'