Exercise 3.13 (Gamma Distribution) Suppose that a continuous random variable has the density function where (x) is the gamma function (3.21). Prove that the MGF

Exercise 3.13 (Gamma Distribution) Suppose that a continuous random variable has the density function

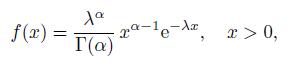
where Γ(x) is the gamma function (3.21). Prove that the MGF is given by

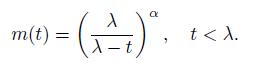
Using this, show that E[X] = α/λ and V[X] = α/λ². Note: An exponential distribution is a special case with α = 1, while the case with α = n/2 and λ = 1/2 corresponds to a chi-square distribution with n degrees of freedom.

f(x) = -xa-e-Ax x > 0, T(a)