Question: A function is homogeneous of degree n when (tx, ty) = t n (x, y). (a) Show that the function is homogeneous and determine

A function ƒ is homogeneous of degree n when ƒ(tx, ty) = tnƒ(x, y).

(a) Show that the function is homogeneous and determine n

(b) Show that xƒx(x, y) + yƒy(x, y) = nƒ(x, y).

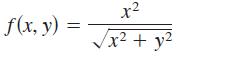
f(x, y) = x x + y

f(x, y) = x x + y

Step by Step Solution

★★★★★

3.30 Rating (168 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a b f x y ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 10th Edition Questions!

Q:

Forensic Accounting Case Study Series - sponsored by Deloitte FAS LLP and the Deloitte Foundation Asset Misappropriation Fraud - Darpa Company Case No. 2-6 Company Overview: Darpa Company ("Darpa" or...

Q:

In convert the following FAs into equivalent PDAs. b b a a a b b

Q:

A function is homogeneous of degree n when (tx, ty) = t n (x, y). (a) Show that the function is homogeneous and determine n (b) Show that x x (x, y) + y y (x, y) = n(x, y). (x, y) = x - 3 2 + y 3

Q:

A function is homogeneous of degree n when (tx, ty) = t n (x, y). (a) Show that the function is homogeneous and determine n (b) Show that x x (x, y) + y y (x, y) = n(x, y). f(x, y) = x2+y2

Q:

A function is homogeneous of degree n when (tx, ty) = t n (x, y). (a) Show that the function is homogeneous and determine n (b) Show that x x (x, y) + y y (x, y) = n(x, y). (x, y) = e x/y

Q:

Call a function ((x, y) homogeneous of degree 1 if ((tx, ty) = t((x, y) for all t > 0. For example, ((x, y) = x + yey/x satisfies this criterion Prove Euler's Theorem that such a function satisfies...

Q:

A function f is homogeneous of degree n when f(tx, ty) = t n f(x, y). In Exercises 39 42, (a) Show that the function is homogeneous and determine n, and (b) Show that xf x (x, y) + yf y (x, y) =...

Q:

A function f is homogeneous of degree n when f(tx, ty) = t n f(x, y). In Exercises 39 42, (a) Show that the function is homogeneous and determine n, and (b) Show that xf x (x, y) + yf y (x, y) =...

Q:

Verify Eq. (11) for the functions in Exercise 44. Data From Exercise 44 A function (x, y, z) is called homogeneous of degree n if (x, y, z) = n (x, y, z) for all R. Show that the following...

Q:

A function (x, y, z) is called homogeneous of degree n if (x, y, z) = n (x, y, z) for all R. Show that the following functions are homogeneous and determine their degree: (a) f(x, y, z) = xy + xyz...

Q:

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

Q:

In a letter to the audit committee of the Cline Wholesale Company, Jerry Schwartz, CPA, informed them of material weaknesses in the control of inventory. In a separate letter to senior management, he...

Q:

Use Adaptive quadrature to find approximations to within 103 for the integrals in Exercise 1. Do not use a computer program to generate these results. 1.5 xedx dx 4 sinx dx e sin 2x da 16 2 24 4...

Q:

A couple used to visit a certain restaurant all of the time to eat a special dish they erjoyed togethec. The couple wert trough a painfal Bresur upa Ater the breakup, one member avoided the...

Q:

Give an example from your field of interest where a paired comparisons test would be appropriate. Use real or realistic data and perform an appropriate hypothesis test.

Q:

Show that the graph of the equation r = -2asin , a > 0, is a circle of radius a with center at (0,-a) in rectangular coordinates.

Q:

Show that the graph of the equation r = 2acos , a > 0 is a circle of radius a with center(a,0) at in rectangular coordinates.

Q:

Show that the graph of the equation r = -2acos , a > 0 is a circle of radius a with center(-a,0) at in rectangular coordinates.

Q:

Oct. 1 A petty cash fund is established with a check for $147.00 issued to the petty cash custodian. 31 A check was written to reimburse the fund and increase the fund to $197.00. A count of the...

Q:

Any relevant income tax and/or capital gains tax implications in relation to the sale of the Strathfield property to Millhouse, arising from the facts down below. In your answer make sure you...

Q:

RMJ KidsRUs Ltd is required to prepare a Cash Flow Statement for the year ended 31 December 2021. Net profit for the financial year is $231,000. 31 December 31 December 2020 2021 Cash $136,000...