In Exercises set up the definite integral for finding the indicated arc length or surface area. Then use the integration capabilities of a graphing utility to approximate the arc length or surface area.

A fleeing object leaves the origin and moves up the y-axis (see figure). At the same time, a pursuer leaves the point (1, 0) and always moves toward the fleeing object. The pursuer's speed is twice that of the fleeing object. The equation of the path is modeled by

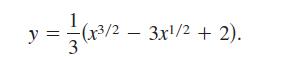
How far has the fleeing object traveled when it is caught?
Show that the pursuer has traveled twice as far.

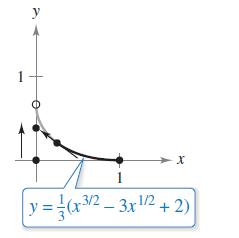
y = =(x3/2 = (x/2 - 3x/2 + 2).