Repeat Exercise 93 for which the exact solution of the differential equation

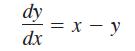
where y(0) = 1, is y = x - 1 + 2e^-x.

Data from in Exercises 93

The exact solution of the differential equation

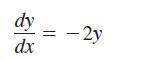
where y(0) = 4, is y = 4e^-2x.

(a) Use a graphing utility to complete the table, where y is the exact value of the solution, y₁ is the approximate solution using Euler's Method with h = 0.1, y₂ is the approximate solution using Euler's Method with h = 0.2, e₁ absolute error |y - y₁|, e₂ is the absolute error |y - y₁|, and r is the ratio e₁/e₂.

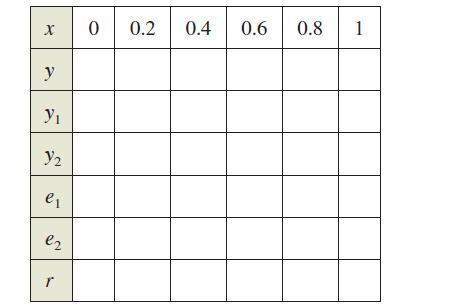
(b) What can you conclude about the ratio r as h changes? 

(c) Predict the absolute error when h = 0.05.

dy dx =x-y