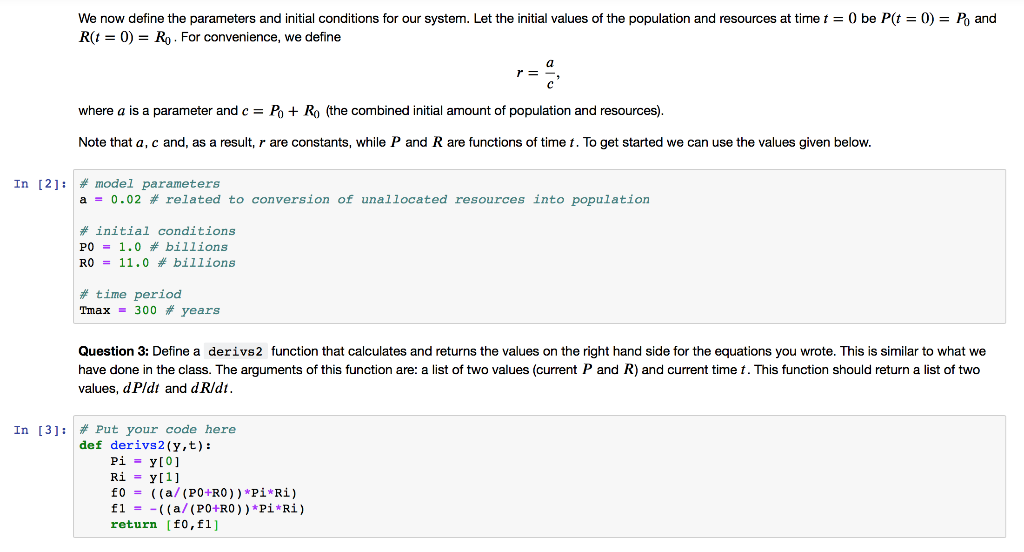
Question: Any thing wrong here? Where? And how to code? We now define the parameters and initial conditions for our system. Let the initial values of

 Any thing wrong here? Where? And how to code?
Any thing wrong here? Where? And how to code?
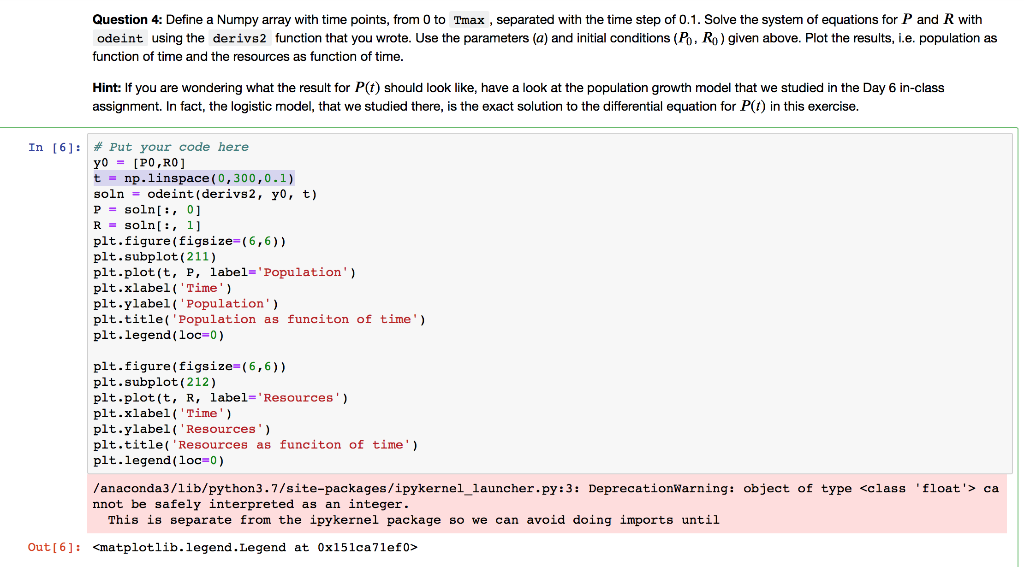
We now define the parameters and initial conditions for our system. Let the initial values of the population and resources at time t = 0 be P(t-0) = P, and R(1-0) = Ro . For convenience, we define r- where a is a parameter and c- PoRo (the combined initial amount of population and resources). Note that a, c and, as a result, r are constants, while P and R are functions of time t. To get started we can use the values given below. In [2]; # model parameters a- 0.02 # related to conversion of unallocated resources into population # initial conditions PO = 1.0 # billions R0 = 11.0 # billions # time period max-300 # years Question 3: Define a derivs2 function that calculates and returns the values on the right hand side for the equations you wrote. This is similar to what we have done in the class. The arguments of this function are: a list of two values (current P and R) and current time t. This function should return a list of two values, d Pldt and dRldt. In [3]: # Put your code here def derivs2(Y,t): Pi - yto1 return [fo,fl Question 4: Define a Numpy array with time points, from 0 to Tmax , separated with the time step of 0.1. Solve the system of equations for P and R with odeint using the derivs2 function that you wrote. Use the parameters (a) and initial conditions (Po, Ro) given above. Plot the results, i.e. population as function of time and the resources as function of time Hint: If you are wondering what the result for P(t) should look like, have a look at the population growth model that we studied in the Day 6 in-class assignment. In fact, the logistic model, that we studied there, is the exact solution to the differential equation for P() in this exercise In [6]. # Put your code here t np.linspace (0,300,0.1) soln-odeint (derivs2, y0, t) R soln[:, 1] plt.figure(figsize-(6,6)) plt.subplot (211) plt.plot(t, P, label- Population') plt.xlabel( 'Time') plt.ylabel Population) plt.title( Population as funciton of time') plt. legend (10c-0 ) plt.figure (figsize- (6,6)) plt.subplot (212) plt.plot (t, R, label- 'Resources') plt.xlabel 'Time) plt.ylabel( 'Resources') plt.title( 'Resources as funciton of time) plt.legend (loc-0) /anaconda3/lib/python3.7/site-packages/ipykernel_launcher.py:3: DeprecationWarning: object of type
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


