Question: A great circle on a sphere S with center O and radius R is a circle obtained by intersecting S with a plane that passes

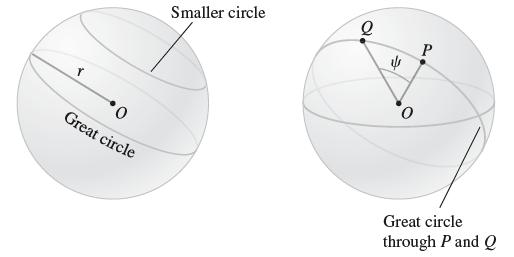
A great circle on a sphere S with center O and radius R is a circle obtained by intersecting S with a plane that passes through O (Figure 19). If P and Q are not antipodal (on opposite sides), there is a unique great circle through P and Q on S (intersect S with the plane through O, P, and Q). The geodesic distance from P to Q is defined as the length of the smaller of the two circular arcs of this great circle.

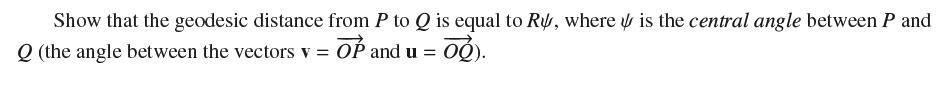
Y 0 Great circle Smaller circle a. S P Great circle through P and Q

Show that the geodesic distance from P to Q is equal to Ry, where is the central angle between P and Q (the

Y 0 Great circle Smaller circle a. S P Great circle through P and Q

Step by Step Solution

★★★★★

3.41 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We place the xycoordinate system in the plane of the great circle determined by P and Q ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Required information [The following information applies to the questions displayed below.] Information on Kwon Manufacturing's activities for its first month of operations follows: a. Purchased...

The magnetic field within a long, straight solenoid with a circular cross section and radius R is increasing at a rate of dB/dt. (a) What is the rate of change of flux through a circle with radius r1...

1. Develop 3 sigma level process control charts for monitoring weight of boxes that contain apples. You performed samplings over 5 weeks with sample size of 4 (n = 4). Draw variable control charts...

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

1.3,7,9, 11, 13, 17, 19, 3.9 EXERCISES 1. If V is the volume of a cube with edge length x and the cube expands as time passes, find dV/di in terms of dx/dt. 3 cm/s. How fast is the x-coordinate of...

1. In the figure two curved plastic rods, one of charge +9 and the other of charge -9, form a circle of radius R = 7.13 cm in an xy plane. The x axis passes through both of the connecting points, and...

The Electric Field Due to an Electric Dipole . 19 Figure 22-40 shows an electric dipole. What are the (a) magni- tude and (b) direction (relative to the positive direction of the x axis) of the...

In the figure two curved plastic rods, one of charge +q and the other of charge -q, form a circle of radius R = 7.72 cm in an xy plane. The * axis passes through both of the connecting points, and...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

Example 1 Show that the volume of a sphere of radius r is V = Solution If we place the sphere so that its center is at the origin (see Figure 4), then the plane Pr intersects the sphere in a circle...

Note: To simplify calculations, you may use g = 10 m/s in all problems.V =7.5 m/s Questions 2-4 refer to the following figure: B C - NWAVAN D velocity (m/s) 1. An object is thrown horizontally to the...

Determine to the nearest percent the IRR on the following projects: a. An initial outlay of $ 10,000 resulting in a free cash flow of $ 2,000 at the end of year 1, $ 5,000 at the end of year 2, and $...

(a) Identify the three types of employer payroll taxes. (b) How are tax liability accounts and payroll tax expense accounts classified in the financial statements?

18-1 Select an activity whose nature is such that it requires the movement of materials or work in process from one work station to another. The activity considered in this and subsequent problems in...

Compute the special taxes for high-income taxpayers.

help with building a smart water meter that consist of combination of based combination wireless,iot and cloud based

Listed below are year end account balances ($ in millions) taken from the records of Symphony Stores Credit 201 Debit 676 939 50 48 25 163 463 36 10 57 Accounts receivable Building and equipment Cash...

If an individual earning $50,000 per year has an opportunity to participate in an employer sponsored 401(k) tax sheltered retirement account with the employer matching the first $1,200 of annual...