Question: Assume that L(a) = lim at - 1 x-0 X exists for all a > 0. Assume also that lim at = 1. x-0

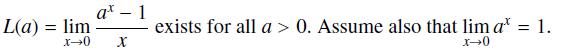
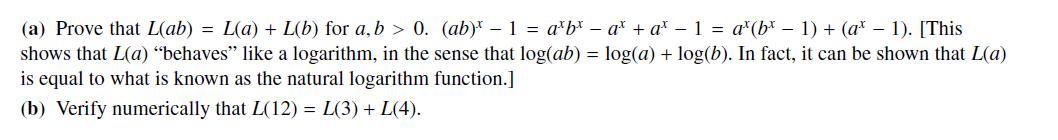
Assume that L(a) = lim at - 1 x-0 X exists for all a > 0. Assume also that lim at = 1. x-0

(a) Prove that L(ab) = L(a) + L(b) for a, b > 0. (ab)* - 1 = a*b* a* + a* - 1 = a*(b 1) + (a* - 1). [This

L(a) = lim at - 1 x-0 X exists for all a > 0. Assume also that lim at = 1. x-0

Step by Step Solution

★★★★★

3.32 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a Let a b 0 Then X Lab lim x0 3x 1x 4 1x 12 1x 001 ab 1 X 1092600 b From the table below ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

What kind of MNC do you think CATL is? Explain your choice.

Q:

The revenues and expenses of Paradise Travel Service for the year ended May 31, 2016, follow: Fees earned $900,000 office expense 300,000 Miscellaneous expense 15,000 Wages expense 450,000 Everett...

Q:

An agreement is reached for an American company to purchase a machine from a foreign vendor for 100,000 euros. At the time of the agreement, the exchange rate is 1.20 dollars per euro. At the time of...

Q:

Assume that Nolanvilles scal year ends on December 31. 1. Nolanvilles payroll for one of its departments is $15,000 per week. It pays its employees on the Thursday of the week following that in which...

Q:

Use the graph to estimate the specified limit. Find lim f(x) and lim f(x) x- (-1) x- (-1)* + 0 -2+ O -7; -5 O -5;-2 O -7;-2 O -2;-7 QUESTION 42 Use the graph to estimate the specified limit. Find lim...

Q:

PLEASE SHOW YOUR EXPLANATION / WORK IN ALL QUESTIONS Question 5 (1 point) () Listen Find the limit, if it exists. lim 10 - x | X - 10 10 - X O -1 Does not existQuestion 6 (1 point) Listen Find the...

Q:

39. [-/7 Points] MY NOTES LARCALC12 1.2.022. ASK YOUR TEACHER Consider the following. X+ 6 lim 2 x=6 x + 13x + 42 Create a table of values for the function. (Round your answers to four decimal...

Q:

Please help me with these problems 5. [-/1 Points] DETAILS LARCALC11 1.3.059. Find the limit. (If an answer does not exist, enter DNE.) lim 7(x + Ax) - 7x AX -0 Ax3. [0\" Points] DETAILS...

Q:

Use the graph below to determine whether the statements about the function x]: are true or false. y: True or false: lim f(x) =4. X- - 2+ O True O False True or false: lim f(x) = 1. X-0- O False O...

Q:

true or false 1. (20%) True or False (a) lim f(x) = L, if f'(a) = L. x->a g(x) g'(a) In(x) (b) For x>10, the ratio approaches 0 as x -> co. Vx-10 (3x3 +12x2 -8x+1) (c) lim = 3. X->00 (x2 +2)(3x-1)...

Q:

WEEK1 LIMITS I. EVALUATE THE LIMIT, IF IT EXISTS. X'+x - 6 x + 5x + 4 9 -t x3- 1 1. lim X -Z x - 2 2. lim X- 4 X2 + 3x - 4 1 9 3 - t 4. x 1 x2 - 1 5. 1 0 t t 2 + t II. FIND THE LIMIT , IF IT EXISTS....

Q:

What process or equipment is used to form rubber compounds into sheets?

Q:

Read the The Monopolistic Competition CC-PP Model (A) For the monopolistic competition model studied in the online manual, based on Krugman, Obstfeld and Melitz (2012), the firms individual demand...

Q:

( 6 - 1 7 ) Investment in Total Net Operating Capital Athenian Venues Inc. just reported the following selected portion of its financial statements for the end of 2 0 2 2 . Your assistant has already...

Q:

Fragile X Syndrome. The second-leading genetic cause of mental retardation is Fragile X Syndrome, named for the fragile appearance of the tip of the X chromosome in affected individuals. According to...

Q:

Let f(x) = (x - 3)-2. Show that there is no value of in (1, 4) such that f(4) - f(1) = f'(c) (4 - 1). Why does this not contradict the Mean Value Theorem?

Q:

Let f(x) = (x - 3)-2. Show that there is no value of in (1, 4) such that f(4) - f(1) = f'(c) (4 - 1). Why does this not contradict the Mean Value Theorem?

Q:

Show that the equation has exactly one real root. 2x + cos x = 0.

Q:

A project's initial fixed asset requirement is $1,620,000. The fixed asset will be depreciated straight-line to zero over a 10 year period. Projected fixed costs are $220,000 and projected operating...

Q:

BUSI 3 5 4 Assignment - Capital Budgeting Santana Inc. manufactures widgets. The end product is produced in different departments within the plant. One component, C 1 , is causing some concern. The...

Q:

Which one yields the highest interest tax shield? The interest rate is 8.5%, A. $10,000 loan with 5 equal annual payments (same total payment each year but composition between interest and principal...