Consider the general logistic function P(t) = M/1 + Ae^−kt , with A, M, and k all positive. Show that

Transcribed Image Text:

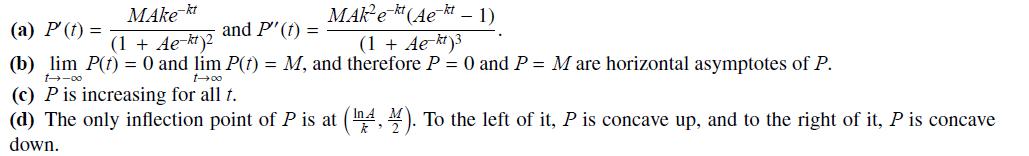
Make-kt MAK-et (Ae-kt - 1) and P' (t) = (1 + Ae-kt)2 (1 + Ae-kt)3 (b) lim P(t) = 0 and lim P(t) = M, and therefore P = 0 and P = M are horizontal asymptotes of P. 1-→-00 1-00 (c) P is increasing for all t. (d) The only inflection point of P is at (4). To the left of it, P is concave up, and to the right of down. (a) P' (t) = P is concave