Consider the integral in Example 1:

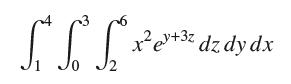
Show that the integrand can be expressed as a product g(x)h(y)k(z). Then verify the equation in Exercise 27 by computing the product of integrals on the right-hand side and showing it equals the result obtained in the example.

Data From Exercise 27

Assume ƒ(x, y, z) can be expressed as a product, ƒ(x, y, z) = g(x)h(y)k(z). Show that the integral of ƒ over a box B = [a, b] × [c, d] × [p, q] can be expressed as a product of integrals as follows:

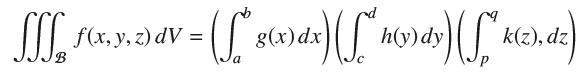
afff x ex+32 dv, where EXAMPLE 1 Integration over a Box Calculate the integral + B= [1,4] x [0, 3] x [2,6].