Question: Given n data points (x 1 , y 1 ), . . . , (x n , y n ), the linear least-squares fit is

Given n data points (x₁, y₁), . . . , (x_n, y_n), the linear least-squares fit is the linear function

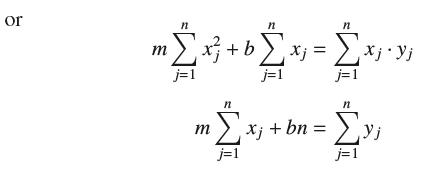
that minimizes the sum of the squares (Figure 26): E(m, b) = ; - f(x;))2 j=1 f(x) = mx + b Show that the

or M m+=; j=1 j=1 j=1 M m x; +bn= j=1 j=1

that minimizes the sum of the squares (Figure 26): E(m, b) = ; - f(x;))2 j=1 f(x) = mx + b Show that the minimum value of E occurs for m and b satisfying the two equations m x; + bn = V; j=1 m j=1 y -- + j=1 j=1 (X2, 32) (1,VD) (Xn, Vn) y = mx + b X

Step by Step Solution

★★★★★

3.38 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

This Excel based project will focus on applications of linear equations and linear least squares regression. Project must be posted as a single PDF file in the provided Assignment DropBox in...

Find the best linear least squares fit of the following data using the indicated weights: (a) (b) (c) (d) .2 4 .7 1.2 21 02 yi -5 -3 2 0 3 .5 2 y 2 13 8 2

When a block of mass M, connected to the end of a spring of mass ms = 7.40 g and force constant k, is set into simple harmonic motion, the period of its motion is T = 2π √M + (ms/3)/k A...

60. Given n data points ($1, y1 ) , . . ., (In, Un), the linear least-squares fit is the linear function f (a) = mx + b that minimizes the sum of the squares (Figure 26): E(m, b) = (y; - f (x;))2...

3. Linear Least-Median Squared algorithm (Algorithm 6.3, page 218 in Jain et al's Machine Vision book). In this problem, use a maximum of 6 trials. Explain how the algorithm below works on the...

Question 1 to 29 a. It is the most familiar and widely used measure of central tendency. b. It is affected by the value of every piece of data. c. It can be computed when data are grouped even if the...

Consider a dataset with n data points (x, y), x, ERP, following the following linear model +t, i=1. where ; N(0,02) are i.i.d. Gaussian noise with zero mean and variance o. (a) (5 points) Show that...

assistance with deriving 3. Locally Weighted Linear Regression and bias-variance tradeoff Consider a dataset with n data points (x,, y;), x, E RP, drawn from the following linear model: vi = B* xi...

Given m data points x', i = 1, ...,m, K-means clustering algorithm groups them into k clusters by mini- mizing the distortion function over {rij, u'} m k J = EEmix - we'll?, (1) i=1j=1 where rij = 1...

Assume that for a given set of n=5 data points (x, y) that exhibit a linear pattern n n n n E xi = 25, E yi = 15, E = 100, and I'M xiyi = 50. i= 1 i=1 i=1 Use the formulae nb + xiyi to determine...

A clock is placed in a satellite that orbits the earth with a period of 90 min. By what time interval will this clock differ from an identical clock on earth after 1 y? (Assume that special...

Think about an organization that you know well. Place the employees of this organization into the following categories: strategic knowledge workers; core employees; supporting workers; and partners...

In a sample of n 5 16 selected from a left-skewed population, X _ 5 65 and S 5 21. Would you use the t test to test the null hypothesis, H0: m 5 60? Discuss.

=+4 Prepare a presentation to the remuneration committee to justify your bonus allocations.

Find the value of each expression if x = 3 and y = -2. ||4x | - |5y||

Find the value of each expression if x = 3 and y = -2. 3|x| + 2|y|

Determine which of the value(s) (a) through (d), if any, must be excluded from the domain of the variable in the expression: (a) x = 3 (b) x = 1 (c) x = 0 (d) x = -1 x - 1

Munoz Car Wash, Inc. expected to wash 1,000 cars during the month of August. Washing each car was expected to require 0.3 hour of labor. The company actually used 305 hours of labor to wash 950 cars....

State whether the propositions in parts (a) through (j) are TRUE or FALSE considering the following sets: X = { a, 1, {a, a}, [a, 1], } Y = { a, 3, {a}, [1, a]} (a) a X (b) {a} X (c) [a, 1] X (d) [a,...

In November 2019, Simon pays $1,000 to take a course to improve his job skills to qualify for a new position at work. Simon's employer reimbursed him for the cost of the course. For 2019, Simon's...