Given positive numbers a1

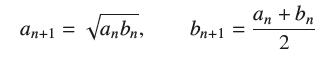
(a) Show that a_n ≤ b_n for all n (Figure 14).

(b) Show that {a_n} is increasing and {bn} is decreasing.
(c) Show that b_n+1 − a_n+1 ≤ b_n − a_n/2.
(d) Prove that both {a_n} and {b_n} converge and have the same limit. This limit, denoted AGM(a₁, b₁), is called the arithmetic-geometric mean of a₁ and b₁.
(e) Estimate AGM(1,√2) to three decimal places.

an+1 = anbn, bn+1 = 11 an + bn 2