Given (x, y) and y = y(x), we can define a composite function g(x) = (x, y(x)). af (a) Show that g'(x) = + af

Given ƒ(x, y) and y = y(x), we can define a composite function g(x) = ƒ(x, y(x)).

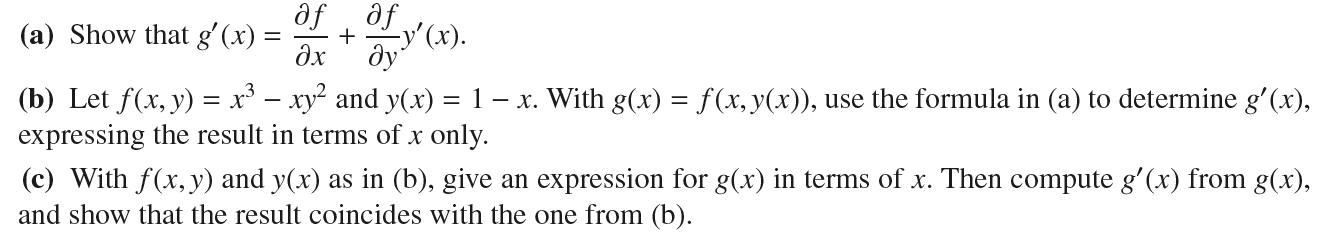
af (a) Show that g'(x) = + af x y'(x). (b) Let f(x, y) = x xy and y(x) = 1 x. With g(x) = f(x, y(x)), use the formula in (a) to determine g'(x), expressing the result in terms of x only. (c) With f(x, y) and y(x) as in (b), give an expression for g(x) in terms of x. Then compute g'(x) from g(x), and show that the result coincides with the one from (b).