Let (x, y) = 4 x 2 y 2 + e 2x and y(x) = e x /x . Define g(x) = (x, y(x)).

Let ƒ(x, y) = 4 − x²y² + e^2x and y(x) = e^x/x . Define g(x) = ƒ(x, y(x)).

(a) Use the derivative formula from Exercise 17(a) to prove that g (x) = 0 and therefore that g is a constant function.

Data From Exercise 17(a)

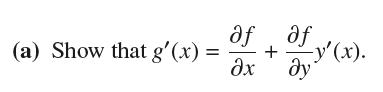
(b) Express g(x) directly in terms of x, and simplify to show that g is indeed a constant function.

(a) Show that g'(x) af af dx + Jy '(x).