Question: If a planet has zero mass (m = 0), then Newtons laws of motion reduce to r (t) = 0 and the orbit is a
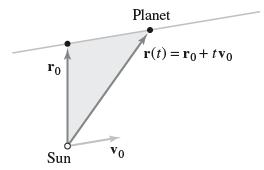
ro Sun Vo Planet r(t) =ro+tvo
Step by Step Solution
3.40 Rating (156 Votes )
There are 3 Steps involved in it
Integrating rt 0 gives The constant c is r0 v0 That ... View full answer

Get step-by-step solutions from verified subject matter experts


