If is continuous on [a, b], then the solution to dy/dt = f (t) with initial condition y(a) = 0 is Show that Eulers

If ƒ is continuous on [a, b], then the solution to dy/dt = f (t) with initial condition y(a) = 0 is 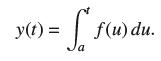 Show that Euler’s Method with time step h = (b − a)/N for N steps yields the Nth left-endpoint approximation to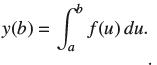 

y(t) = [ f(u) du.