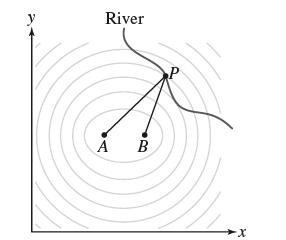
Question: In a contest, a runner starting at A must touch a point P along a river and then run to B in the shortest time
In a contest, a runner starting at A must touch a point P along a river and then run to B in the shortest time possible (Figure 17). The runner should choose the point P that minimizes the total length of the path.
(a) Define a function![]() Rephrase the runner’s problem as a constrained optimization problem, assuming that the river is given by an
Rephrase the runner’s problem as a constrained optimization problem, assuming that the river is given by an
equation g(x, y) = 0.
(b) Explain why the level curves of ƒ(x, y) are ellipses.
(c) Use Lagrange multipliers to justify the following statement: The ellipse through the point P minimizing the length of the path is tangent to the river.
(d) Identify the point on the river in Figure 17 for which the length is minimal.
f(x, y) = AP + PB, where P = (x, y)
Step by Step Solution
3.49 Rating (152 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


