Question: In Example 1, we found the maximum of (x, y) = 2x + 5y on the ellipse (x/4) 2 + (y/3) 2 = 1. Solve

In Example 1, we found the maximum of ƒ(x, y) = 2x + 5y on the ellipse (x/4)² + (y/3)² = 1. Solve this problem again without using Lagrange multipliers. First, show that the ellipse is parametrized by x = 4 cos t, y = 3 sin t. Then find the maximum value of ƒ(4 cos t, 3 sin t) using single-variable calculus. Is one method easier than the other?

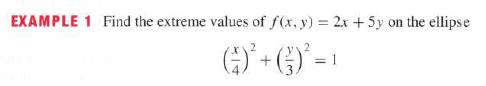
EXAMPLE 1 Find the extreme values of f(x, y) = 2x+5y on the ellipse (-) + ( ) = 1

EXAMPLE 1 Find the extreme values of f(x, y) = 2x + 5y on the ellipse (-) + (-) = 1

Step by Step Solution

★★★★★

3.49 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We want to find the maximum of fx y 2x 5y on the ellipse 4 1 without using Lagrange multipliers Cons... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Case analysis and discussion 5 : Winning a War Without an Armor: Tesla s Open Innovation Strategy in Emerging Markets ( pages 4 1 2 - 4 1 7 ) No unread replies. No replies. Answer all the QUESTIONS...

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

a. Example 13-1: Batch Reactor with an Exothermic Reaction Wolfram 1. Adiabatic Case: Use Wolfram to see whether you can find a trajectory that is ready to ignite and whose trajectory looks like a...

List three specific parts of the Case Guide, Objectives and Strategy Section (See below) that you had the most difficulty understanding. Describe your current understanding of these parts. Provide...

878 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES (e) Does P correspond to a minimum or maximum value of f? Re- fer to Figure 12 to justify your answer. Hint: Do the values of f(x, y) 2 increase or...

Module 4 - Case SYSTEMS OF EQUATIONS AND INEQUALITIES Assignment Expectations Complete the following problems using the Case 4 Answer Template. 1.What are the 3 methods for solving systems of...

Question 18 1pts A Z score is also a percentile rank. True False Flag this Question Question 19 1pts Regression lines are used for comparison of two variables to determine similarity. True False Flag...

3 inches Matched structed from 288 square box with the largest possible volume 6 inches 9 inches CONCEPTUAL INSIGHT Figure 8 An alternative to the method of Lagrange multipliers would be to solve...

D 1. Graph the solution set of the system of inequalities or indicate that the system has no solution. x2 + _'.=2 =81 -2x + 5y =-10 10 D 2. Solve the linear programming problem. Mrs. White wants to...

Math 012 Midterm Exam Fall 2017 Professor: Dr. Liz Grubert Name________________________________ Instructions: The exam is worth 75 points. There are 15 questions, each worth 5 points. Your score on...

Which of the following ratios is the best measure of liquidity? a. Return on assets ratio. b. Cash flow from operations to capital expenditures ratio. c. Current ratio. d. Earnings per share.

What is the best way to answer the question, Tell me about yourself?

In Exhibit 14, the opportunity cost of wheat is a. 1/3 ton of potatoes in the United States and 1/2 ton of potatoes in Ireland. b. 2 tons of potatoes in the United States and 1 1/2 tons of potatoes...

What are environmental forces? AppendixLO1

Prove the statement. (1 + a) n 1 + na, for a > 0

Show that the statement n 2 n + 41 is a prime number is true for but is not true for n = 41.

Show that the formula 2 + 4 + 6 + + 2n = n 2 + n + 2 obeys Condition II of the Principle of Mathematical Induction.That is, show that if the formula is true for some k it is also true for Then show...

what are the responsibilities of the software project manager

Last month when Holiday Creations, Incorporated, sold 45,000 units, total sales were $180,000, total variable expenses were $140,400, and fixed expenses were $35,800. 1. What is the companys...

Determine the average rate of return for a project that is estimated to yield total income of $568,980 over six years, has a cost of $595,100, and has a $58,900 residual value. Round to the nearest...