In the parametrization c(t) = (a cos t, b sin t) of an ellipse, t is not an angular parameter unless a = b (in which case, the ellipse is a circle). However, t can be interpreted in terms of area: Show that if c(t) = (x, y), then t = (2/ab)A, where A is the area of the shaded region in Figure 29.

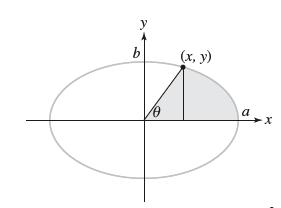
The area S₂ under the curve can be computed using Eq. (9). The lower limit of the integration is t₀ = 0 (corresponds to (a, 0)) and the upper limit is t (corresponds to (x(t), y(t))). Also y(t) = b sin t and x'(t) = −a sin t. Since x'(t)

Combining (1) and (2) we obtain

Hence, t = 2A/ab.

y b 0 (x, y) a X