Question: Let a, b, r be constants. Show that is a general solution of y = Cekt + a + bk dy dt = k sin

Let a, b, r be constants. Show that

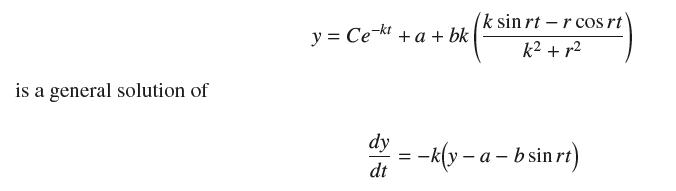
is a general solution of y = Cekt + a + bk dy dt = k sin rt-r cos rt k + r -k(y - a - b sinrt)

is a general solution of y = Cekt + a + bk dy dt = k sin rt-r cos rt k + r -k(y - a - b sinrt)

Step by Step Solution

★★★★★

3.46 Rating (149 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

This is a linear differential equation in standard form it i... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Assuming that the cost of goods manufactured is $3,460,000 compute the cost of goods sold using the following information. Raw materials inventory, January 1 $ 30,000 Raw materials inventory,...

Q:

In the absence of free charge or free current, the Maxwell equations in optically active matter are (a) Let P = ( 0)E and M = ( 1 0 1)B, but do not introduce D or H. Assume plane wave behavior...

Q:

Let A B R, let f : B R and let g be the restriction of f to A (that is, g(x) = f(x) for x A). (a) If f is continuous at c A, show that g is continuous at c. (b) Show by example that if g is...

Q:

1. A point charge q with mass m is released from rest at the origin in an external magnetic field and an external electric field. Both of the external fields are uniform but the electric field points...

Q:

I need answers for questions 7-9 You notice that the flow of the water alternates between two flows that we'll call flow 1 and flow 2. The x and y coordinates are as shown above. The velocity v of...

Q:

SOLVE Questions 1-5: PLEASE AND THANK YOU 1: What is the difference between homogenous and non-homogenous differential equation? Write an example for each and solve it. 2: What is the main formula to...

Q:

1. 3 2 Consider the function f(x) = x - 3x - 9x + 10, x (a) . Find the equation of the straight line passing through the maximum and minimum points of the graph y = f(x). (4) (b) Show that the point...

Q:

question 1 Find the partial derivative of the dependent variable with respect to each of the independent variables. Z= (3x2 + x/3)7 dz = 7(3x2 + xy3, 6(6* + 3) dzThe volume V of a right circular...

Q:

hello mighty tutors , this is my final test !!! need a good cualification to pass the class !! hope you acan help me !! there is 15 math problems !!! help me obi wan kenobi , you are my only hope !!!...

Q:

10 Green's functions for PDEs In this final chapter we will apply the idea of Green's functions to PDEs, enabling us to solve the wave equation, diffusion equation and Laplace equation in unbounded...

Q:

Mark Miller started a moving company on January 1, 2016. On March 1, 2016, Miller borrowed cash from a local bank by issuing a one-year $80,000 face value note with annual interest based on a 12...

Q:

A machine that costs $8,000 is expected to operate for 10 years. The estimated salvage value at the end of 10 years is $0. The machine is expected to save the company $1,554 per year before taxes and...

Q:

which decay process is possible? 2 2 4 Ra - > 2 2 8 Th + a 1 4 C - > 1 4 N + e ^ - + Ve 1 3 7 Ba * - > 1 3 7 Ba + y

Q:

(a) What value of R2 is required so that a regressionwith five independent variables is significant if there are 30 observations? [Hint: Use the 0.05 critical value for F(5,24)]. (b) Answer part (a)...

Q:

If cos = 0.2, find the value of: cos + cos( + 2) + cos( + 4 )

Q:

If tan = 3, find the value of: tan + tan( + ) + tan( + 2)

Q:

If cot = -2, find the value of: cot + cot( - ) + cot( - 2)

Q:

If $16800 is deposited in a savings account today, what amount will be available three years from today? The following future value interest factors are provided:...

Q:

In an open economy with few capital restrictions and substantial import-export trade, and rise in interest rates and a decline in the producer price index of inflation will

Q:

Can anyone help me solve this problem? Here is a clear photo Compute the IRR statistic for Project F. The appropriate cost of copital is 13 percent. (Do not round intetmediate calculatiens and round...