Let (a) Show that there is a unique point P = (a, b) on g(x, y) = 1 where P = gP for some scalar

Let 

(a) Show that there is a unique point P = (a, b) on g(x, y) = 1 where ∇ƒP = λ∇gP for some scalar λ.
(b) Refer to Figure 13 to determine whether ƒ(P) is a local minimum or a local maximum of ƒ subject to the constraint.
(c) Does Figure 13 suggest that ƒ(P) is a global extremum subject to the constraint?

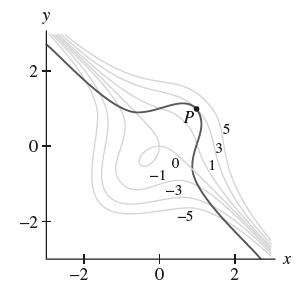
f(x, y) = x + xy + y, g(x, y) = x - xy +y