Let be a function whose graph does not pass through the x-axis and let Q = (a, 0). Let P = (x 0 ,(x

Let ƒ be a function whose graph does not pass through the x-axis and let Q = (a, 0). Let P = (x₀,ƒ(x₀)) be the point on the graph closest to Q (Figure 5). Prove that PQ is perpendicular to the tangent line to the graph of x₀. Find the minimum value of the square of the distance from (x, ƒ (x)) to (a, 0).

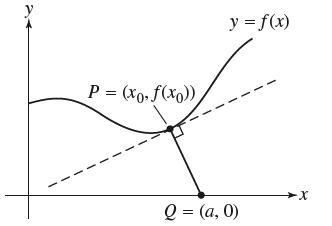
P = (xo, f(xo)), y = f(x) Q = (a,0)