Use Exercises 64 and 65 to prove the following assertions for all x ≥ 0 (each assertion follows from the previous one):

Data From Exercise 64

Prove that if ƒ(0) = g(0) and ƒ'(x) ≤ g'(x) for x ≥ 0, then ƒ(x) ≤ g(x) for all x ≥ 0. Show that the function given by y = ƒ(x) − g(x) is nonincreasing.

Data From Exercise 65

Use Exercise 64 to prove that x ≤ tan x for 0 ≤ x

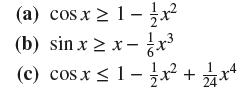
Can you guess the next inequality in the series?

(a) cos x 1-x (b) sinx > x-x (c) cos x 1-x + 2/4x4