Let be an increasing function on [a, b] and let g be its inverse. Argue on the basis of arc length that the following

Let ƒ be an increasing function on [a, b] and let g be its inverse. Argue on the basis of arc length that the following equality holds:

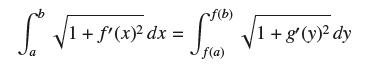
Then use the substitution u = ƒ(x) to prove Eq. (4).

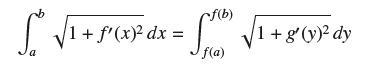
f(b) S* = [ 1 + f'(x) dx a f(a) 1 + g' (y) dy