Suppose that the observer in Exercise 62 moves off to infinity—that is, d → ∞. What do you expect the limiting value of the observed area to be? Check your guess by using the formula for the area in the previous exercise to calculate the limit.

Data From Exercise 62

Prove that the portion of a sphere of radius R seen by an observer located at a distance d above the North Pole has area A = 2πdR²/(d + R). According to Exercise 52, the cap has surface area 2πRh. Show that h = dR/(d + R) by applying the Pythagorean Theorem to the three right triangles in Figure 22.

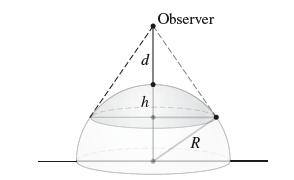
Data From Exercise 52

Show that a spherical cap of height h and radius R (Figure 19) has surface area 2πRh.

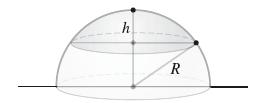
h Observer R