Question: Let I n = x n dx/x 2 + 1. (a) Prove that In = x n1 1 I n2 . (b) Use

Let In = xn dx/x2 + 1.

(a) Prove that In = xn−1  − 1 − In−2.
(b) Use (a) to calculate In for 0 ≤ n ≤ 5.
(c) Show that, in general,

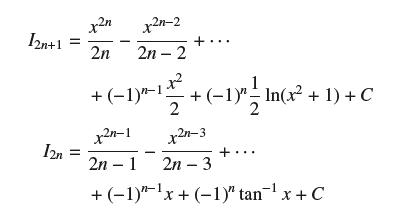
12n+1 = 12n = xn 2n x2n-2 2n - 2 12 + (1)- + (1)1 In(x + 1) + C 2 x2n-1 x2n-3 2n - 1 2n-3 + (-1)"x + (-1)"

12n+1 = 12n = xn 2n x2n-2 2n - 2 12 + (1)- + (1)1 In(x + 1) + C 2 x2n-1 x2n-3 2n - 1 2n-3 + (-1)"x + (-1)" tan x + C

Step by Step Solution

★★★★★

3.34 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a I dx fx1 dx xdx S x 1 b First compute Io and I directly 12 x dx dx Io 1 21 tanxC and ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-6. On December 12, Irene purchased the building where her store is located. She paid...

Q:

A 0 . 7 5 - m x 1 . 5 - m window is constr cted of 6 - mm - thick glass. On a cold night, the inside and outside surface temperatures of the glass are 1 6 deg C and - 2 4 deg C , respectively. ( a )...

Q:

When President Obama was President he had discussed raising income taxes for individuals earning over $250,000 in income. Explain how these higher income taxes will affect the aggregate demand curve....

Q:

Part 1 Portfolio Return and Risk Instruction: You are a portfolio investment analyst at Goldman Sachs. Your investment unit manages two equity portfolios - one portfolio, named P1, consists of two...

Q:

115.109 Topic 7 Lab Worksheet: Comparing Means Latest due date: October 9 In this lab we return to the dataset used in Week 4 (the Countdown customer dataset) to investigate differences in mea There...

Q:

1. Show that for f(x) : 2+ ex + (e 1)sin (1%). f'(x) is 0 at least once in the interval [0,1]. 2. Let f(X) = (1 X)'1 and X0 = 0. Find the nth Taylor Polynomial Pn(X) for f(x) about x0. Find a value n...

Q:

sign (or type) your name below the following honor pledge: I have completed this quiz by myself, working independently and not consulting anyone except the instructor. I have neither given nor...

Q:

1. (10 points) Show that the set N x N ((0,0), (0, 1),... is countable. Note that if you use picture to demonstrate correspondence and need to skip some elements, you must explain in what situation...

Q:

If the Number of communications channels required for a team is calculated using the formula N(N-1)/2, where N is the number of stakeholders, if there are 5 stakeholders, then there must be 5(5-1)/2...

Q:

The formula to calculate the communication channels is: n x (n - 1) / 2. N is the number of team members. Use the formula to determine the number of communication channels for a team of five members....

Q:

Sally and Sabrina are partners in a shoe business. As Sally works full time in the business, they agree that Sally will receive an annual salary of $50,000, and thereafter, that all profits are to be...

Q:

Paramel Beverages bottles two soft drinks under licence to Cadaver Ltd. at its Newcastle plant. Bottling at this plant is highly repetitive, automated process. Empty bottles are removed from their...

Q:

Refer to the graph provided. a. Which point(s) could represent a downturn in the business cycle? b. Which point(s) represent efficient production? c. Which point(s) are attainable only after long-run...

Q:

19. Expand Your Knowledge: Two Confidence Intervals What happens if we want several confidence intervals to hold at the same time (concurrently)? Do we still have the same level of confidence we had...

Q:

In problem, approximate each number using a calculator. Express your answer rounded to three decimal places. e 1.2

Q:

In problem, the function f is one-to-one. Find the inverse of each function and check your answer. f(x) = 3/x 1/3

Q:

After the release of radioactive material into the atmosphere from a nuclear power plant at Chernobyl (Ukraine) in 1986, the hay in Austria was contaminated by iodine 131 (half-life 8 days). If it is...

Q:

Find a business that uses first come, first served & last come, first served for their business? a. What are the pros and cons of each?

Q:

budgeted production is it a receipt or payments in cash budget?

Q:

Harvard Business Case: What do you predict will happen to Gap Inc.s sales going forward as a result of this decision? How will it affect each of its brands equity? Link to case:...