Question: Let (mathcal{S}) be the oriented half-cylinder in Figure 15. In (a)-(f), determine whether (iint_{mathcal{S}} mathbf{F} cdot d mathbf{S}) is positive, negative, or zero. Explain your

Let $\mathcal{S}$ be the oriented half-cylinder in Figure 15. In (a)-(f), determine whether $\iint_{\mathcal{S}} \mathbf{F} \cdot d \mathbf{S}$ is positive, negative, or zero. Explain your reasoning.
(a) $\mathbf{F}=\mathbf{i}$
(b) $\mathbf{F}=\mathbf{j}$
(c) $\mathbf{F}=\mathbf{k}$
(d) $\mathbf{F}=y \mathbf{i}$
(e) $\mathbf{F}=-y \mathbf{j}$
(f) $\mathbf{F}=x \mathbf{j}$

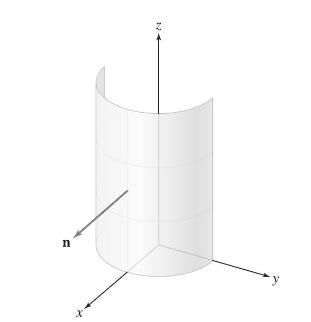
n X N

Step by Step Solution

★★★★★

3.34 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

S is parametrized by Phitheta zcos theta sin theta z quad 0 leq z leq 3 quadfracpi2 leq theta leq fracpi2 Hence beginaligned mathbfTtheta fracpartial ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Area Under a Curve The area under the graph of y = 1/1 x 2 and above the x-axis between x = a and x = b is given by sin 1 b sin 1 a. See the figure. X x = -1 -1 a Ay x = 1 I 1 b 1 X

Question 7 Russell Company uses a job-order costing system and began the month of March with three jobs in process. The cost of beginning work in process plus the costs added during March are given...

The diagram shows a rhombus ABCD. M is the midpoint of BD. a. Find the coordinates of M. b. Find the value of a, the value of b and the value of c. c. Find the perimeter of the rhombus. d. Find the...

Let $\mathbf{F}=\langle z, 0, yangle$, and let $\mathcal{S}$ be the oriented surface parametrized by $\Phi(u, v)=\left(u^{2}-v, u, v^{2}ight)$ for $0 \leq u \leq 2$, $-1 \leq v \leq 4$....

Let $\mathcal{S}$ be the surface of the cylinder (not including the top and bottom) of radius 2 for $1 \leq z \leq 6$, oriented with outward-pointing normal (Figure 16). (a) Indicate with an...

Let $\mathcal{S}$ be the surface with parametrization \[ \Phi(u, v)=\left(\left(1+v \cos \frac{u}{2}ight) \cos u,\left(1+v \cos \frac{u}{2}ight) \sin u, v \sin \frac{u}{2}ight) \] for \(0 \leq u...

EAS Let $\mathcal{S}$ be the surface with parametrization \[ \Phi(u, v)=((3+\sin v) \cos u,(3+\sin v) \sin u, v) \] for $0 \leq u \leq 2 \pi, 0 \leq v \leq 2 \pi$. Using a computer algebra...

Let $\mathcal{S}$ be the half-cylinder $x^{2}+y^{2}=1, x \geq 0,0 \leq z \leq 1$. Assume that $\mathbf{F}$ is a horizontal vector field (the $z$-component is zero) such that \(\mathbf{F}(0,...

Potential Due to a Uniform Sphere Let $\mathcal{S}$ be a hollow sphere of radius $R$ with its center at the origin with a uniform mass distribution of total mass $m$ [since $\mathcal{S}$ has...

Let $\mathbf{F}=\left\langle y,-x, x^{2}+y^{2}ightangle$, and let $\mathcal{S}$ be the portion of the paraboloid $z=x^{2}+y^{2}$ where $x^{2}+y^{2} \leq 3$. (a) Show that if $\mathcal{S}$...

Using the state space analysis technique, obtain the stat model of the mechanical system shown in Fig. 8. F(t) B, M2 Y2 K2 B2 Fig. 8

Identify and discuss the trade-offs associated with operating a supply chain that handles both forward and reverse movement as compared with separate supply chains for forward and reverse movement.

31. LO.2, 3 Innovation, Inc., a 501(c)(3) medical research organization, makes lobbying expenditures of $1.1 million. Innovation incurs exempt purpose expenditures of $15 million in carrying out its...

To what extent does inclusion in a consumer decision set by a destination represent a source of advantage?

Let andconsider the Trapezoid Rule (T(n)) and the Midpoint Rule (M(n)) approximations to I. a. Compute T(6) and M(6). b. Compute T(12) and M(12). 1 = Sox dx = 9

Evaluate the following integrals. dx (x 1)4 -00

Evaluate the following integrals. dx xe

For this part of the assignment, you will only be modeling part of the information - the academic information that must be kept about each student. Be sure to read the entire case for context and...

A firm has sales of $4,680 costs of $2,480, interest paid of $163, and depreciation of $461. The tax rate is 21 percent. What is the cash coverage ratio?

I am in group 4 i need this presentation tomorrow before before 5 pm please send me as soon as possible it is for 10% and Course name is Business Reports and Presentations Due Date: Week 4 (Written)...