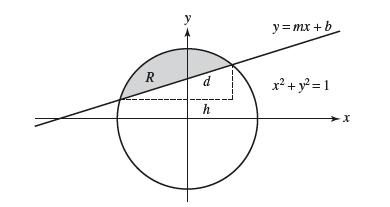
Question: Let R be the region in the unit circle lying above the cut with the line y = mx + b (Figure 20). Assume that

Let R be the region in the unit circle lying above the cut with the line y = mx + b (Figure 20). Assume that the points where the line intersects the circle lie above the x-axis. Use the method of Exercise 65 to show that the solid obtained by rotating R about the x-axis has volume V = π/6 hd², with h and d as in the figure.

R y d h y=mx+b x + y=1 X

Data From Exercise 65

R y d h y=mx+b x + y = 1 X

Step by Step Solution

★★★★★

3.33 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Let x and x denote the xcoordinates of the points of intersection ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

The Pratt roof trusses shown in Figure Ql are uniformly spaced every 6 m . The deck, roofing material and the purlins have an average weight of DL kN / m ? . The building is located. in city centre...

Let R be the region in the first quadrant bounded by the curves y = x3 and y = 2x x2. Calculate the following quantities. (a) The area of R (b) The volume obtained by rotating R about the x-axis (c)...

Let R be the region in the first quadrant below the curve y = X-2/3 and to the left of x = 1. (a) Show that the area of R is finite by finding its value. (b) Show that the volume of the solid...

Consider each of the following unrelated cases, involving the ownership of shares of Canadian-controlled private corporations. Assume all of the issued shares are common shares unless specifically...

Your last submission is used for your score. 1. [-/1 Points] DETAILS LARCALC11 15.4.008. Verify Green's Theorem by evaluating both integrals 10 v2 ax + x 2 dy = Jel ON aM dA ay for the given path. C:...

175 Homework B Section 6.3 (Part II) 1 of 3 https://www.webassign.net/web/Student/Assignment-Responses/last?dep... WebAssign 175 Homework B Section 6.3 (Part II) (Homework) Current Score : - / 5...

Hello. I recently took an exam. The teacher gave us the solutions to the exam. However, I am still confused on questions 2, 4, 6, 7, and 10. I attached the exam down below, cold you explain them to...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

*solve the attached4 questions. 15. Let /(x) =e-2' (a) Find any horizontal and vertical asymptotes of f(r). (b) Find the intervals where f(7) is increasing and the intervals where f (7) is...

6 | Consumer Choices Figure 6.1 Investment Choices Higher education is generally viewed as a good investment, if one can afford it, regardless of the state of the economy. (Credit: modification of...

Five large letters should be spread out evenly across a banner. The banner is 14 feet wide. Each letter is 2 feet wide. The letters touch the banner's left and right edges (no margins). How much...

Draw the net electric field vectors at points A, B, and C. The orientation of your vectors will be graded. The exact lengths of your vectors will not be graded. No elements selected 92

State of the economy Probability HPR Boom . 3 1 8 % Normal growth . 5 1 2 % Recession . 2 - 5 % What is the expected standard deviation for KMP stock? Group of answer choices 6 . 9 1 % 8 . 1 3 % 7 ....

What do we mean by lifestyle? What factors determine and influence lifestyle?

Let c1, c2 ,...... cn, en be positive constants with And let x1, x2, ..........., xn be positive numbers. Take natural logarithms and then use l'Hopital's Rule to show that 12 1/r 12 lim (axby)yb

Verify the last statement in Problem 46 by calculating each of the following? (a) (b) (c) 10

Consider f(x) = n2xe-nx? (a) Graph f(x) for n = 1, 2, 3, 4, 5, 6 on [0, 1] in the same graph window? (b) for x > 0. Find limn( f(x). (c) Evaluate (d) Guess at f(x) dx for n I , 2. 3. 4. 5. 6. lim...

A 7-year callable bond has a coupon rate of 5% (paid semi-annually). The total term of the bond is 7 years but the bond is callable in 3 years with a prepayment penalty of 1 years coupon interest...

For each company, calculate the missing amount. (Please note, this company has No non-operating expenses or revenues.)

Required information [The following information applies to the questions displayed below] On January 1,2024 , Ocean World issues $39.1 million of 9% bonds, due in 20 years, with interest payable...