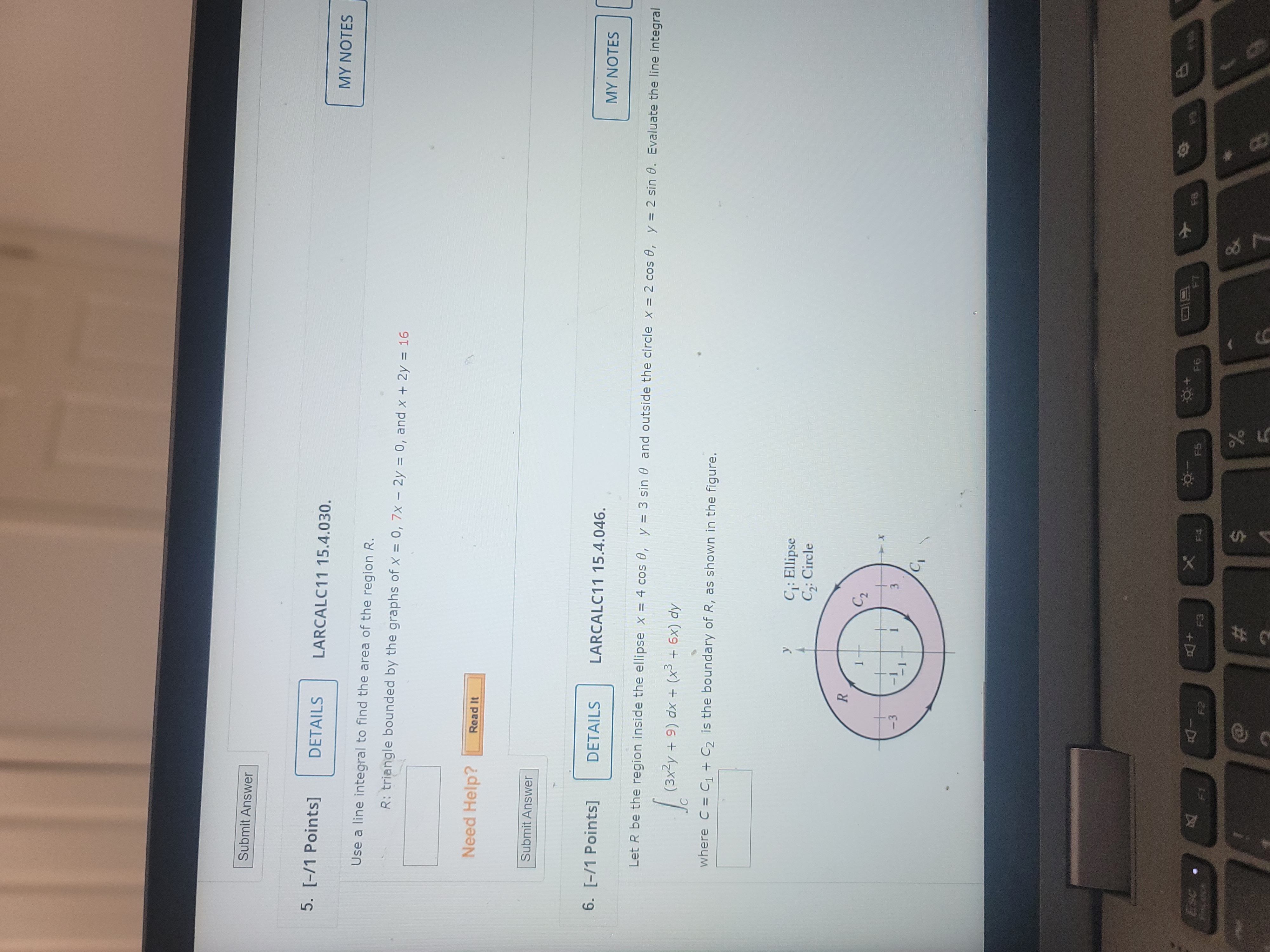
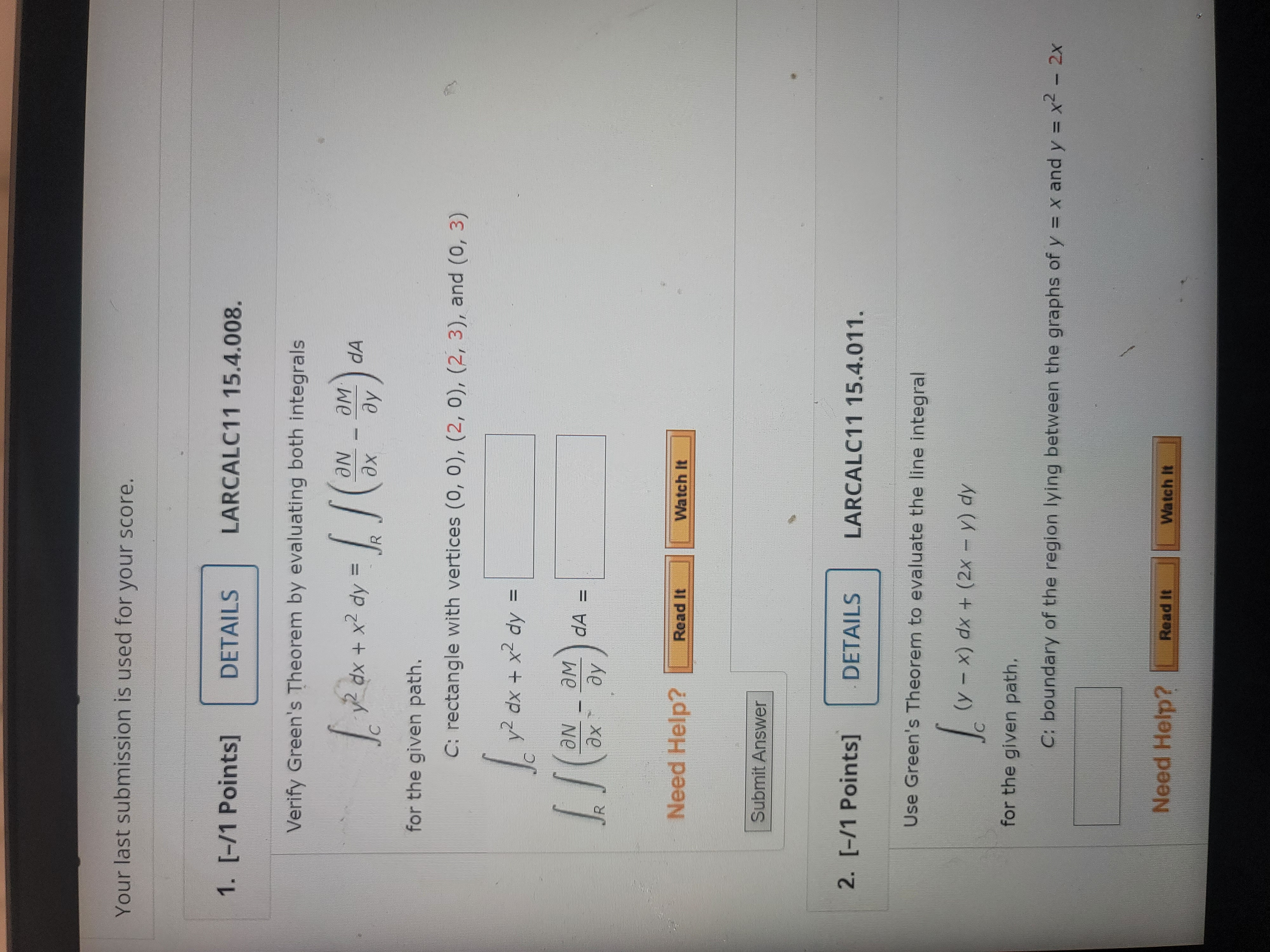
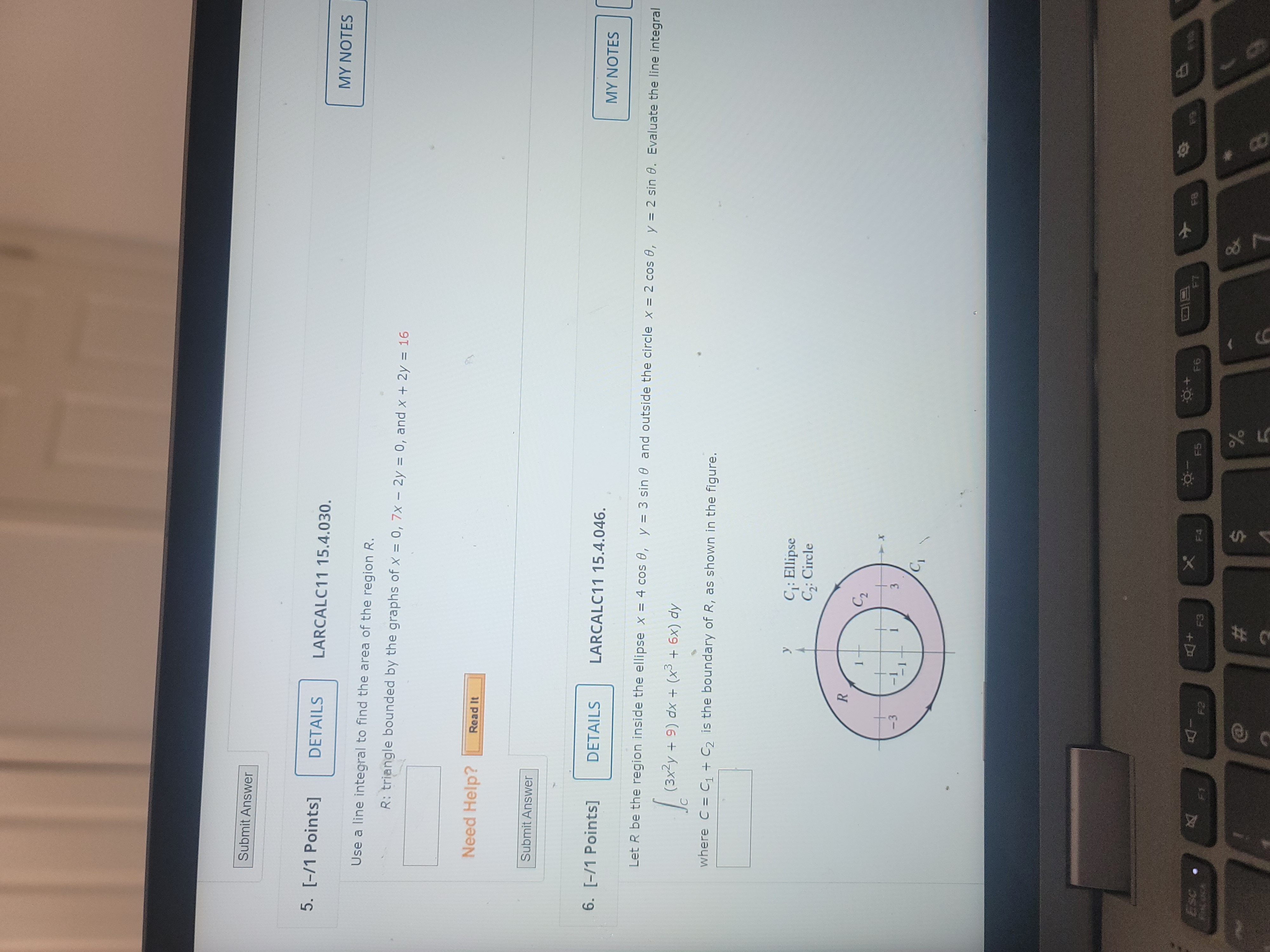
Your last submission is used for your score. 1. [-/1 Points] DETAILS LARCALC11 15.4.008. Verify Green's Theorem by evaluating both integrals 10 v2 ax + x 2 dy = Jel ON aM dA ay for the given path. C: rectangle with vertices (0, 0), (2, 0), (2, 3), and (0, 3) 12 dx + x2 dy = ON _ aM ax- dy dA = R Need Help? Read It Watch It Submit Answer 2. [-/1 Points] . DETAILS LARCALC11 15.4.011. Use Green's Theorem to evaluate the line integral ( * - x ) dx + ( 2x - y ) dy for the given path. C: boundary of the region lying between the graphs of y = x and y = x2 - 2x Need Help? Read It Watch ItNeed Help? Read It Watch It Submit Answer 3. [-/1 Points] DETAILS LARCALC11 15.4.016. Use Green's Theorem to evaluate the line integral. 1 2 dx + xy dy C: boundary of the region lying between the graphs of y = 0, y = vx, and x = 9 Need Help? Read It Watch It Submit Answer 4. [-/1 Points] DETAILS LARCALC11 15.4.023. Use Green's Theorem to evaluate the line integral. ( x - 5y ) dx + ( x + y ) dy C: boundary of the region lying between the graphs of x7 + y2 = 1 and x2 + y2 = 25 Need Help? Read it Watch ItSubmit Answer 5. [-/1 Points] DETAILS LARCALC11 15.4.030. MY NOTES Use a line integral to find the area of the region R. R: triangle bounded by the graphs of X = 0, 7x - 2y = 0, and x + 2y = 16 Need Help? Read It Submit Answer 6. [-/1 Points] DETAILS LARCALC11 15.4.046. MY NOTES Let R be the region inside the ellipse x = 4 cos 0, y = 3 sin 0 and outside the circle x = 2 cos 0, y = 2 sin 0. Evaluate the line integral ( ( 3 x 2 4 + 9 ) dx + ( * 3 + 6 x ) dy where C = Cj + C2 is the boundary of R, as shown in the figure. C: Ellipse C2: Circle R X FS FO F2 F3 F4 S %