Let (x) be a function of one variable defined near x = a. Given a number M, set e(x) = f(x) - L(x) e(x) L(x)

Let ƒ(x) be a function of one variable defined near x = a. Given a number M, set

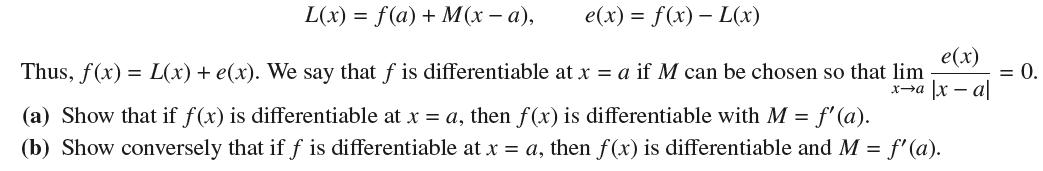
e(x) = f(x) - L(x) e(x) L(x) = f(a) + M(x a), Thus, f(x)=L(x) + e(x). We say that f is differentiable at x =a if M can be chosen so that lim xa |xa| (a) Show that if f(x) is differentiable at x = a, then f(x) is differentiable with M = = f'(a). (b) Show conversely that if f is differentiable at x = a, then f(x) is differentiable and M = f'(a). = 0.