Question: Let (x) = sin(x 2 ) and I = 1 0 (x) dx. (a) Check that f'(x) = 2 cos(x) - 4x sin(x). Then

Let ƒ(x) = sin(x²) and I = ∫¹₀ƒ(x) dx.

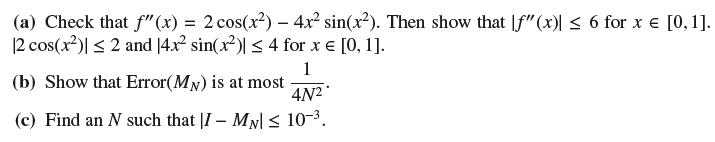
(a) Check that f'(x) = 2 cos(x) - 4x sin(x). Then show that f

(a) Check that f'(x) = 2 cos(x) - 4x sin(x). Then show that f"(x)| 6 for x = [0, 1]. 12 cos(x)| 2 and 14x sin(x)| 4 for x [0, 1]. 1 (b) Show that Error(MN) is at most 4N (c) Find an N such that I - MN| 10-.

Step by Step Solution

★★★★★

3.37 Rating (147 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Taking derivatives we get On the interval 0 1 fx 2x cosx fx 2x... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Among infants who have experienced birth trauma, A) sleep behavior is organized and patterned B) disturbed REM-NREM sleep cycles are often present C) REM sleep is filled with vivid dreams D)...

Alejandro Puron recently encountered a dilemma in working with his quality circle (QC) team. One of the team members claims that the QC must always be unanimous in its recommendations....

3. For the given translational mechanical system shown in the figure, Obtain the transfer function, X1(s)/F(s). (1)!r + 5 N/m 4 N-s/m 5 kg Figure Figure

. Question 17 2 pts Let f(x) = x + 3 and g(x) - 3x2 + 2x. Calculate the composition below and simplify the result. (go f) (x) =Question 18 2 pts 9 1 0 Details Suppose the graph of y = x is stretched...

Symbolic answers must be entered using notation similar to the examples given below. If you enter decimal numbers for questions that indicate that a symbolic answer is required, it will be marked as...

Which one is correct, and which one is wrong? Give reasons for your answers. a. b. x 2x lim x-0x sin x = = 2x - 2 lim x-02x lim x-02 2 COS X sin x = 2 2 +0 || 1

Verify the identity. COS x - sin x = 2 cos - x - 1 Which of the following four statements establishes the identity? O A. 2 cos * x - sin X =cos *x - (1- cos

If f x sin 6x 2 then f x 0 Note The inverse of sin x can be entered as arcsin r or asin

Let X = 3 0 1 0 2 1 0 3 1 1 0 1 . (a) Show that XX is positive definite. (b) Calculate (XX)1. Is it also positive definite? (c) If y = 3231 , what is ???? = (XX)1Xy?What is u = y X???? ?

The curve C has parametric equations x = sin t, y = cos 2t + 1, 0

A share of stock is expected to pay a dividend of $1.00 one year from now and grow at 5% thereafter. In the context of a dividend discount model, the stock is correctly priced today at $10. According...

A bearing has a specific dynamic radial capacity of 40 kN. The desired life is 5000 hours for 90% of the bearings. The equivalent radial load at 400 rev/min is (a) 8.11 kN (b) 9.43 kN (c) 10.27 kN...

Do the following Problems: Program for Regular Expressions: Create a Python program that will open myFile.txt Read the lines and then print each line that ends in the letters " EX " or has the letter...

Guarantee: Battery Life Many people consider their smart phone to be essential! Communication, news, Internet, entertainment, photos, and just keeping current are all conveniently possible with a...

Between 12:00 PM and 1:00 PM , cars arrive at Citibanks drive-thru at the rate of 6 cars per hour (0.1 car per minute). The following formula from statistics can be used to determine the probability...

If f(x) = a x , show that f(-x) = 1/f(x).

The normal healing of wounds can be modeled by an exponential function. If A 0 represents the original area of the wound and if A equals the area of the wound, then the function A(n) = A 0 e -0.35n...

What is the interest expense ratio for ACME bank? Taxes are 5000 and non interest expense is 5000 Provision for loan losses 10000

The Lefty Golf Co. reported Credit Sales of $4,000,000 at year-end of 2022. The balance sheet at 12/31/2021 reported Accounts Receivable of $450,000, and $550,000 at 12/31/2022. What was the Accounts...

A table has 1,000,000 (million) rows. Each row is 500 bytes. - The data transfer speed of the disk is 400 MB/SEC - The seek time is on average 0.001 seconds - The index fan out is 200 - The secondary...