Question: Prove in two ways that the numbers m(a) satisfy m(ab) = m(a) + m(b) (a) First method: Use the limit definition of m(b) and (b)

Prove in two ways that the numbers m(a) satisfy m(ab) = m(a) + m(b)
(a) First method: Use the limit definition of m(b) and

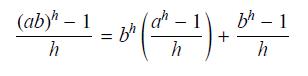
(aby)" - 1 = b" (a^ = 1) + b = 1 - - Bh h h h

(b) Second method: Apply the Product Rule to axbx = (ab)x.

(ab)" - 1 = B (r^= -1) + b = 1 - Bh h h

Step by Step Solution

★★★★★

3.44 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a mab lim h0 lim h0 ab 1 h ah h 1 lim h0 lim bh ah1 h ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Module 6 Instructions Follow the instructions for Problem Set 1 and Problem Set 2 . Use SPSS to complete steps 1, 2, and 3, then use your SPSS Output and Graphs to complete step 4. Paste the required...

Q:

The movie cinematic industry is not what it once was. Back in the 1 9 4 0 s , a trip out to the theater was a common occurrence. The typical American saw 2 8 films a year in the theater. Now, that...

Q:

5) a) Consider a processor with two levels of cache with the following properties: L1 Hit rate: 90%, L1 Access (hit): 4 cycles, L2 Hit Rate: 80%, L2 Access (hit): 12 cycles, DRAM Hit Rate: 100%, DRAM...

Q:

List three specific parts of the Case Guide, Objectives and Strategy Section (See below) that you had the most difficulty understanding. Describe your current understanding of these parts. Provide...

Q:

After reading CHAPTER 2 below from Michael J. Sandel 's book " JUSTICE ", please answer the following question: QUESTION: What are the strengths of Bentham 's thinking on moral reasoning? CHAPTER 2:...

Q:

Lab 23 CSIS 10A Fractions The purpose of an object in a programming language is to represent things that cannot be represented using a single primitive data types such as int, double, char, boolean....

Q:

CHE 405 Dr. Grunenfelder HW 3 Due: 9/18/15 (beginning of class) Excel spreadsheets for the data sets in this assignment can be downloaded from blackboard (assignments folder: HW3 spreadsheet). For...

Q:

Matlab There are a variety of methods for calculating pi. These all involve computing an infinite series, so you can't calculate the exact value of pi, but the more terms you compute, the better the...

Q:

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Q:

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Q:

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Q:

Frederick Consulting had just landed a white whale of a customer, Wilfrid Laurier University, after spending $52,000 in initial acquisition costs! Laurier is expected to generate $39,000 a year in...

Q:

In Java, the report.txt must list the students sorted by either the gpa or number of credit hours. Use the Java Comparator interface to sort the students. For that, copy the Student objects into an...

Q:

When we decompose any expression into ( left expression ) operation ( right expression ) the expression tree of that expression is the binary tree whose Question 1 options: root contains the...

Q:

1. What experience do you have, such as work history and companies with which you have been associated?

Q:

Using calculus, determine the effect of an increase in the price of beef, pb, from $4 to $4.60 on the equilibrium price and quantity in the Canadian pork example. (Conduct an analysis that differs...

Q:

Due to a recession that lowered incomes, the 2008 market prices for last-minute rentals of U.S. beachfront properties were lower than usual. Suppose that the inverse demand function for renting a...

Q:

Lewit and Coate (1982) estimated that the price elasticity of demand for cigarettes is -0.42. Suppose that the daily market demand for cigarettes in New York City is Q = 20,000p-0.42 and that the...

Q:

During the audit of financial statements, an auditor discovers that the financial statements might be materially misstated due to the existence of fraud. Describe (1) the auditors responsibility...

Q:

The three standard methods of appraisal of real estate are comparable value, cost of reproducing the improvements and the income approach. Discuss the the three approaches in terms of the users of...

Q:

You expect to have the given amount in an account with the given terms. Find how much you can withdraw periodically in order to make the account last the specified amount of time. Round your answer...