Prove that if r(t) takes on a local minimum or maximum value at t 0 , then r(t 0 ) is orthogonal to r'(t 0

Prove that if ΙΙr(t)ΙΙ takes on a local minimum or maximum value at t₀, then r(t₀) is orthogonal to r'(t₀). Explain how this result is related to Figure 11. Observe that if r(t₀) is a minimum, then r(t) is tangent at t₀ to the sphere of radius ΙΙr(t₀)ΙΙcentered at the origin.

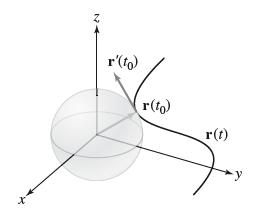
N r'(to) r(to) r(t)