Prove that the function (x, y) = 1/3 x 3 + 2/3 y 3/2 xy satisfies (x, y) 0 for x 0

Prove that the function ƒ(x, y) = 1/3 x³ + 2/3 y^3/2 − xy satisfies ƒ(x, y) ≥ 0 for x ≥ 0 and y ≥ 0.

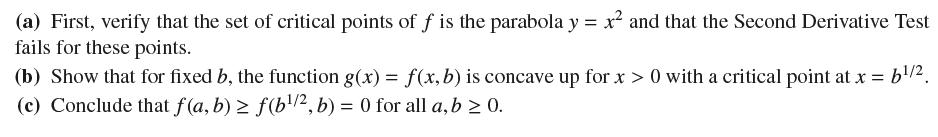
(a) First, verify that the set of critical points of f is the parabola y = x and that the Second Derivative Test fails for these points. (b) Show that for fixed b, the function g(x) = f(x, b) is concave up for x > 0 with a critical point at x = b/2 (c) Conclude that f(a, b) f(b/, b) = 0 for all a, b 0.