Show directly, as in Exercise 43, that (x, y) = xy 2 is differentiable at (0, 2). Data From Exercise 43 This exercise shows directly

Show directly, as in Exercise 43, that ƒ(x, y) = xy² is differentiable at (0, 2).

Data From Exercise 43

This exercise shows directly (without using Theorem 1) that the function ƒ(x, y) = 5x + 4y² from Example 1 is differentiable at (a, b) = (2, 1).

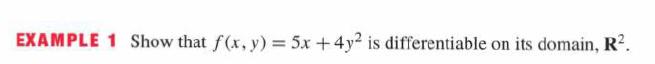
THEOREM 1 Confirming Differentiability If fx(x, y) and fy(x, y) exist and are con- tinuous on an open disk D, then f(x, y) is differentiable on D.