Show that (t) = 1/2 (t 1/2) is a solution to dy/dt = t 2y. Sketch the four solutions with y(0) = 0.5,

Show that ƒ(t) = 1/2 (t − 1/2) is a solution to dy/dt = t − 2y. Sketch the four solutions with y(0) = ±0.5, ±1 on the slope field in Figure 11. The slope field suggests that every solution approaches ƒ(t) as t → ∞. Confirm this by showing that y = ƒ(t) + Ce^−2t is the general solution.

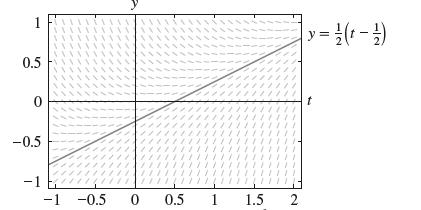
1 0.5 0 -0.5 -1 -1 -0.5 0 0.5 1 1.5 2 y = 1/2(t-1) t