Question: Show that there does not exist a function (x, y) such that = (y 2 , x). Use Clairauts Theorem xy =

Show that there does not exist a function ƒ(x, y) such that ∇ƒ = (y2, x). Use Clairaut’s Theorem ƒxy = ƒyx.

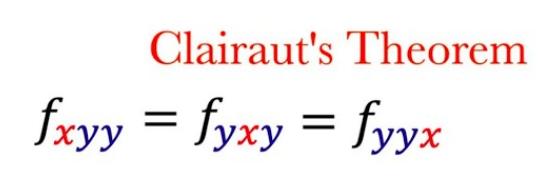
Clairaut's Theorem fxyy = fyxy = fyyx

Clairaut's Theorem fxyy = fyxy = fyyx

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

Suppose that for some differentiable function fx y Of f... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Use the argument in the proof of Theorem 2.1.4 to show that there does not exist a rational number s such that s2 = 6.

Q:

Show that there does not exist any number c such that the following function would be a p.f.: for x = 1, 2, . 0 otherwise f(x) r tor x-1.2

Q:

Show there does not exist a continuously differentiable function f on [0, 2] such that f(0) = -1, f(2) = 4, and f(x)

Q:

SECTION 15.5 24. f (x, y) = sin(x - y), v= (1,1), P = (5, 6) 45. Use the geostrophi 25. f (x, y ) = tan-1 (xy), v = (1,1), P = (3,4) ern Hemisphere, winds together the isobars, 26. f (x, y ) = exy...

Q:

IIIIIIIIII IIIIIIIIIII Find the first partial derivatives of the function. 9 f(X, y) 4 + 4xy f (x, y ) = f (x, y) = VVerify that the conclusion of Clairaut's theorem holds, that is, u = U xy yx 4 U =...

Q:

These are the practice problems for the final exam, the answers are there, I just want to know how to solve them? So can you please show to me the solving steps for each question! MATH 1720/1760...

Q:

calculate below questions and provide easy step format thankyou. (1) Consider the following system of linear equations, ax - 2y +2 = I + ay + 2z = a where a E R is a parameter. (a) Classify the above...

Q:

- L o Show all working and reduce solutions to the simplest form. 1. [9 marks] Differentiate the following functions; (a) f(x) = r**tanx (b) g[x) = 2335in]; L4 ( y(x) = Fx 2. [6marks] A farmer wants...

Q:

1. (10 pts each) Use the Boolean Postulates and Theorems (table 2.2 of the textbook) to simplify the following expressions as far as possible. Show and justify each step by citing the theorem or...

Q:

D F G K L Hturn Z X C V B N M ) - x In(y?). 1xx(2.3) north. The angle D between magnetic north and true north is called the magnetic declination. Use Figure 10 to determine which of the following...

Q:

Right Now Video Inc. uses a lean manufacturing strategy to manufacture DVR (digital video recorder) players. The company manufactures DVR players through a single product cell. The budgeted...

Q:

Referring to Problem 18-12, assume the Ajax managers determine any issues identified by the control charts were caused by one time events. The data for weeks 41 through 45 are in the Ajax-Extra file....

Q:

Suppose the interest rate of a revolving loan account is 0.8 % per month and interest is compounded monthly. Then the corresponding APR is Answer Question 8 %

Q:

=+A number of regional councils (which cover the towns served by the small and large rural branches) have expressed concern over reports that AusBank is considering closing some of its 568 Chapter...

Q:

Use a graphing utility to graph the functions R given in Problem. Verify the solutions found above. .3 x + 2x2 + x R(x) 4 x* + x' + 2x + 2 .3

Q:

Use a graphing utility to graph the functions R given in Problem. Verify the solutions found above. x - 3x? + 4x 12 x* - 3x + x 3 R(x)

Q:

Name three functions that are continuous at every real number.

Q:

explain the difference between a flat file database model and a relational model. Elaborate why you believe a relational model will better suit cheetah deliveries

Q:

Matty Kim, an accountant for Vernitron, earned $109,300 from January to June. In July Matty earned $20,000. Assume a tax rate of 6.2 for Social Security on $113,700 and 1.45% on Medicare. How much is...

Q:

Algorithm DoSomething (A[0..n-1]) 1. value