Suppose that functions and g satisfy Eq. (1) and have the same initial valuesthat is, (0) = g(0) and '(0) = g(0). Prove that

Suppose that functions ƒ and g satisfy Eq. (1) and have the same initial values—that is, ƒ(0) = g(0) and ƒ'(0) = g(0). Prove that ƒ(x) = g(x) for all x. Apply Exercise 70(a) to ƒ − g.

Eq.(1)

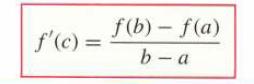
Data From Exercise 70

Suppose that ƒ(x) satisfies the following equation (an example of a differential equation):

(a) Show that ƒ(x)²  + ƒ'(x)² = ƒ(0)² + ƒ'(0)² for all x. Show that the function on the left has zero derivative.

f'(c) = f(b)-f(a) b-a